A couple more diagrams on axe balance.

[FortyTwoBlades]

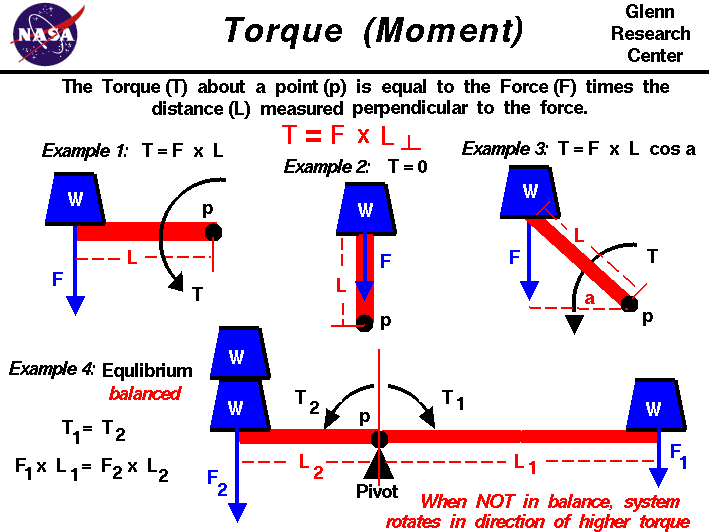
I post this in the full knowledge that it may rankle a sensitive few because some of my assertions on tool balance run counter to popular established lore. However romantic a notion that lore might be, both the theory and application of these concepts is based on pretty basic/simple physics and geometry that you can easily test yourself, and provide more concrete and pragmatic reasoning for the form of axes and other hand tools throughout history and across the globe. I consider this valuable information for anyone looking to gain a deeper understanding of the interplay of axe and handle design or looking to make their own handles. If you doubt my assertions you can easily confirm these principles with very minimal testing, and the beauty of it is that no familiarity with mathematics is required--just plumb lines and your own hands.

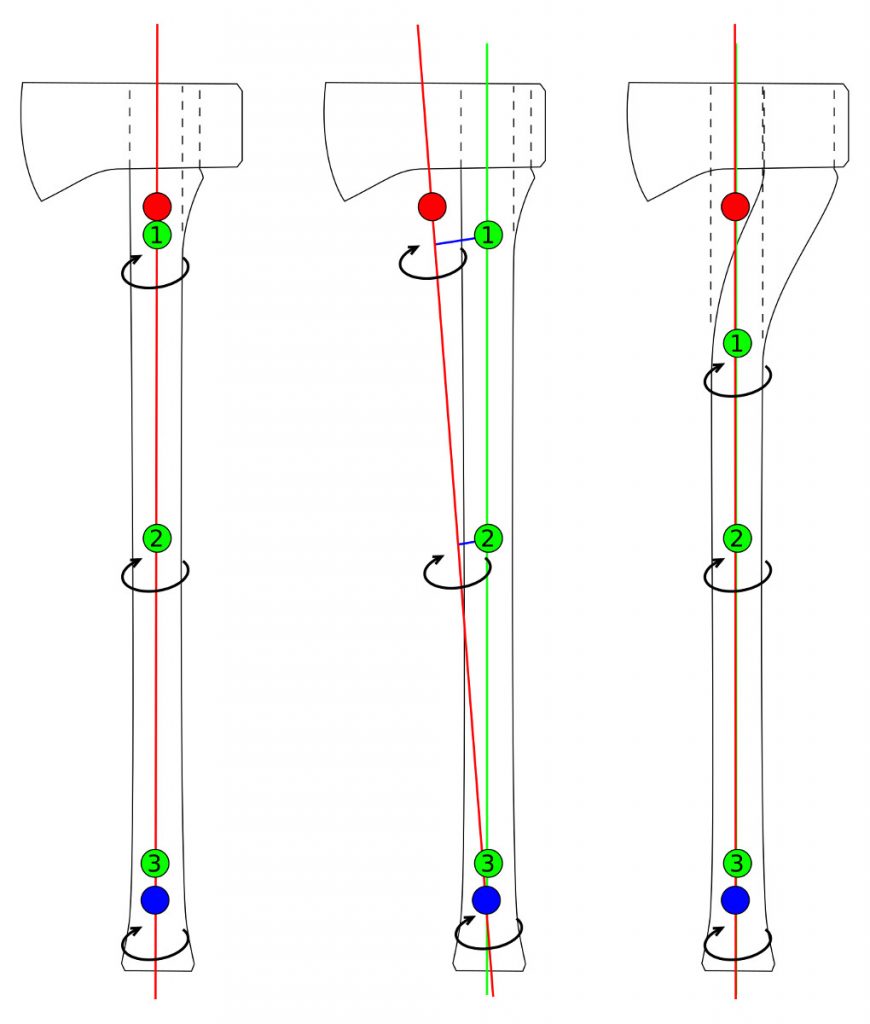
The above show the axle of the tool (red line) and corresponding lever arms (blue lines in center figure) of the tool when used with a sliding upper hand (numbered green dots) and fixed lower hand (blue dot.) As in previously posted diagrams, the red dot shows the center of gravity, and when the axle and handle diverge, the axis along which the hand is sliding is shown by a green line.

On the left you can see that the axe head is balanced by its large poll, and so a straight handle is an appropriate match, with no imbalances imparting torque on the hand in horizontal blows.

The middle axe has the same profile, but the eye has been shifted to the far rear, causing the center of gravity to shift forward in response. This now causes the handle to run off-axis and we can see the lever arms imparting torque on the axle at different points along its length as the upper hand position changes during a sliding stroke. As the hands converge we can see that the lever arm gets shorter and shorter until it becomes essentially insignificant. As such, the infamous “wobble” of a poll-less axe is mostly imparted at the beginning of the stroke, and–while not the ideal–if bearing this in mind it can be compensated for in technique by applying appropriate counter-torque at the start of the stroke and making the slide as early in the stroke as possible.

The third axe now shows the poll-less head with the handle corrected to bring the main length back along a unified axle. This axe will afford the bit size-to-head-weight advantages of a poll-less axe with mostly equal balance to the polled version. One will note that while the axe will now balance properly, the upper hand cannot go as high on the handle as the straight one without running off-axis again. The handle also is trickier to make than in the case of the other two examples and requires better grain alignment to minimize runout.

In case the previous diagrams (here and elsewhere where I've written previously) have been a little difficult to visualize, this diagram simplifies the relationship by eliminating complicating factors. Rather than an “axe” shaped head, we have a simple long, eyeless bar as if the handle were welded to the solid head. The top view shows us the forces at work when the axe is held horizontal. The intersection of the handle’s trajectory and the centerline of the head is shown by the red circle, and the handle treated as massless. A triangle is placed at the point of rotation to indicate the fulcrum forced by the two-point grip. The two sides of this “teeter-totter” are colored to assist in seeing their relative length, and the lines are copied and shown below the head for a clearer comparison.

In the first figure we see a balanced “T” shape, with mass being equally distributed to either side of the center of gravity, and the handle running directly towards it. This tool is in perfect rotational balance.

In the second figure, the handle has been shifted to one side and the lever arms are now imbalanced, causing the longer end to want to drop. The hollow magenta circle marks the center of gravity and the dotted line indicates where the axe would be rotating from if held by the bottom hand only. With the second hand in play, the forced axle of the red line is where the axe will rotate when held/suspended loosely. However, torque applied along the red line will cause the tool to attempt to rotate around the natural axle of the dotted line.

In the third figure, the handle is now offset to align the handle with the natural axle. The red dotted line shows where the handle had previously run in the second figure. The lever arms are now brought back into balance and the “teeter-totter” is now equalled out again.

I've posted them before, but post them here again as a demonstration of the theory applied to actual physical axes. Some of them came out a little blurry but I haven't had a chance to retake them (along with plumb line shots of the axes in question) due to other responsibilities and the frequent rain we've been having, but will do so when I get the opportunity.

A Council 3.5lb Classic Jersey:

Because the mass is equally distributed to either side of the axis formed by the two contact points, the axe balances dead level when held horizontally. The handle is already aligned with the center of gravity, thanks to the large poll putting the balance point of the head inside the eye. No correction needed to optimize the balance. This is a physical example of the axes in the first figure of both diagrams above.

A Rinaldi "Trento" pattern axe with the factory handle:

The large, deep bit and minimal poll means that the head is inherently bit heavy. Because the factory handle runs behind the center of gravity, the bit wants to "droop". This isn't a problem in making downward cuts, but you have to correct for it in use when making horizontal cuts. This is an example of the axes in the second figure of the diagrams above.

The same Trento pattern with a custom offset handle (about 90% fitted) that aligns the main length of the handle with the center of gravity. I very much enjoy using this axe, so the custom handle was worth the effort.

​

Because the main gripped length of the handle now aligns with the center of gravity, the axe now balances horizontally just like the Council, despite it having a minimal poll.

 

[Woodcraft]

I post this in the full knowledge that it may rankle a sensitive few because some of my assertions on tool balance run counter to popular established lore.

No, several of your previous assertions run counter to facts. Like, Most American axes a plumb line falls in front of the handle/eye." Or "the Council tool classic Jersey has perfect balance." That one is funny because it runs counter to the first claim,, and this one "there is no such thing as perfect balance."
But carry on..........

 

[FortyTwoBlades]

For anyone that's missed prior written work on the subject, there's the full blog post here. The two diagrams and their respective descriptions have been added to the end of the document.

Edit to add: For anyone curious about some previous back-and-forth drama that's sprung up over this, these threads are a couple of notable examples.

 

[Square_peg]

The middle axe has the same profile, but the eye has been shifted to the far rear, causing the center of gravity to shift forward in response. This now causes the handle to run off-axis and we can see the lever arms imparting torque on the axle at different points along its length as the upper hand position changes during a sliding stroke. As the hands converge we can see that the lever arm gets shorter and shorter until it becomes essentially insignificant. As such, the infamous “wobble” of a poll-less axe is mostly imparted at the beginning of the stroke, and–while not the ideal–if bearing this in mind it can be compensated for in technique by applying appropriate counter-torque at the start of the stroke and making the slide as early in the stroke as possible.

I hadn't thought of it exactly that way but your logic follows. This is why an off balance axe is less accurate in felling operations and demonstrates why fellers preferred the balanced double bit axe.

During the stroke the needed counter-torque is changing as the upper hand slides. You're essentially aiming at a moving target.

 

[FortyTwoBlades]

Fortunately the amount of counter-torque needed is reducing as the hand slides, so that's not something that needs much accounting for, but especially if you make your slide in a short burst at the beginning of the stroke it gets the need for it minimized as rapidly as possible and maximizes the time you have for any wobble present to correct itself. Almost like how the "archer's paradox" gives the most trouble at short range and corrects itself over distance. But certainly any steps taken to minimize it are of an advantage, and yes, it's likely one of the major factors why fellers enjoyed double bits so much. Depending on the head and how well the owner "grokked" handle design they could put together a single bit that balanced as well as a DB, but it's really simple with a DB because all you do is slap a straight handle in the eye and you're good to go. No figuring needed.

 

[Steve Tall]

Fortunately the amount of counter-torque needed is reducing as the hand slides...

This seems to be a misconception. For "the middle axe" in the top diagram, the (small-polled) unbalanced axe head causes a certain amount of torque (or "moment") that needs to be resisted by the hands that hold the axe handle horizontally. [This torque can be calculated, in foot pounds, by multiplying the weight (in pounds) by the distance (in feet) from the center of mass to the axis of the handle (the green line).] This torque on the handle (resulting from the unbalanced head) stays the same, no matter where on the green line the handle is gripped. Therefore, "the amount of counter-torque needed" also stays the same.

 

[FortyTwoBlades]

I don't think so, but would be happy to learn a thing or two if I'm wrong on that point. Think of it this way--in the second set of diagrams, as the hand slides down the handle you'd basically have the fulcrum triangle in the top view sliding back towards the center position the closer to the bottom you got. You can already see that in effect with the corrected handle whereby the two grip points are fully converged along the main stretch of the handle length and because they're "on top of each other" in a top-down view you don't have any torque occurring.

Additionally the amount of wobble that is able to be induced by the top hand applying force out of alignment with the stroke is reduced as the lever arm decreases. When providing counter-torque, in any case, it works best to deliver it from the fixed bottom hand, as it ensures the most stable stroke. The amount you have to apply from there remains stable and that hand doesn't have to loosen in order to slide.

 

[FortyTwoBlades]

As a note, the custom handle on the Trento shown at the end of the OP was done by applying the described principles digitally. I snapped a photo of the axe and traced it using a vector program, scaled that tracing up to 1:1, used the plumb line method to find the center of gravity, marked it on the image, and then manipulated the handle shape until I had something that gave it a unified axle while still having an appropriate presentation of the bit and fitting inside the size of my boards. Then I printed the image, cut it out, and glued it to the hickory board, cut the blank according to the template, and then all I did was knock it down from a rectangular cross section to what would pass through the eye. And, voila, it balanced horizontally just as expected.

 

[Steve Tall]

I don't think so, but would be happy to learn a thing or two if I'm wrong on that point. Think of it this way--in the second set of diagrams, as the hand slides down the handle you'd basically have the fulcrum triangle in the top view sliding back towards the center position the closer to the bottom you got...

Further explanation:
Imagine the axe handle is a shaft, and the axe head is an unbalanced wheel that's welded to the shaft, and it wants to rotate a quarter-turn as you hold the shaft in your two hands, but you keep the shaft from rotating. No matter where on the shaft you hold it, the unbalanced wheel torques the shaft the same amount, the torque doesn't magically go away, and you still have to resist the rotation.

About that second set of diagrams, a big difference (from the first set) is that the middle one is drawn such that the final position of the hands is approximately at the place they'd be for the perfectly balanced case. To get this result, either the straight handle is not actually straight at the eye, or else the eye would have to be crooked. This is not a good representative case.

 

[FortyTwoBlades]

Further explanation:
Imagine the axe handle is a shaft, and the axe head is an unbalanced wheel that's welded to the shaft, and it wants to rotate a quarter-turn as you hold the shaft in your two hands, but you keep the shaft from rotating. No matter where on the shaft you hold it, the unbalanced wheel torques the shaft the same amount, the torque doesn't magically go away, and you still have to resist the rotation.

About that second set of diagrams, a big difference (from the first set) is that the middle one is drawn such that the final position of the hands is approximately at the place they'd be for the perfectly balanced case. To get this result, either the straight handle is not actually straight at the eye, or else the eye would have to be crooked. This is not a good representative case.

Actually, the torque WOULD go away when the center of gravity was directly above or below said shaft. And as the hands got closer together, you'd be reducing your "L" measure shown below:

The whole point of the second image is having the bottom hand in the same spot regardless of the run of the handle and how the different alignments impact the position of the sliding hand. In the case of a "crooked eye" you'll notice that most deep-bitted poll-less axes actually have pretty closed sets to the bits because the bit needs to remain in proper alignment with the radius of the arc it's traveling on. Remember that the handle was described as attaching to a solid, eyeless head of uniform shape, as if being welded to it. It's a deliberately simplified form to make the visualization easier rather than being an actual idealized axe shape. If you were to tilt the middle "axe" (that more resembles a mallet) so that the handle were then vertical you'd see that the head was comparatively closed. This is specifically because of keeping the presentation of the bit relative to the lower hand the same is important. I'm wondering what exactly makes you think it's not a suitable example when trying to simplify the presentation?

 

[Steve Tall]

Actually, the torque WOULD go away when the center of gravity was directly above or below said shaft...

Yes, that's obvious and irrelevant. If you hold the axe vertically (as for bucking), then of course there is no torque. But the diagrams and discussions are about axes being held horizontally.

You haven't really addressed my example of the unbalanced wheel welded to a shaft, which illustrates how the torque WOULD NOT go away for the middle axe.

Actually, the torque WOULD go away when the center of gravity was directly above or below said shaft....

The whole point of the second image is having the bottom hand in the same spot regardless of the run of the handle and how the different alignments impact the position of the sliding hand. In the case of a "crooked eye" you'll notice that most deep-bitted poll-less axes actually have pretty closed sets to the bits because the bit needs to remain in proper alignment with the radius of the arc it's traveling on. Remember that the handle was described as attaching to a solid, eyeless head of uniform shape, as if being welded to it. It's a deliberately simplified form to make the visualization easier rather than being an actual idealized axe shape. If you were to tilt the middle "axe" (that more resembles a mallet) so that the handle were then vertical you'd see that the head was comparatively closed. This is specifically because of keeping the presentation of the bit relative to the lower hand the same is important. I'm wondering what exactly makes you think it's not a suitable example when trying to simplify the presentation?

I thought it was being overly simplified, but now re-reading the post I see your mentions of the simplifications, so I retract those specific comments about that second set of diagrams.

 

[FortyTwoBlades]

You haven't really addressed my example of the unbalanced wheel welded to a shaft, which illustrates how the torque WOULD NOT go away for the middle axe.

I did, though. You'd be reducing the distance of the force from the pivot. That reduces the torque.

Edit: To clarify, torque experienced on the handle closer to the head remains unchanged. However, your hand is moving to a point on the handle that experiences less torque.

 

[Woodcraft]

If you have fixed the horizontal bit heavy problem you would be able to show that with a one finger balance test. You can not. I own a Classic Jersey from council, they are bit heavy. HORIZONTAL AND VERTICAL. LOL.

 

[Steve Tall]

I did, though. You'd be reducing the distance of the force from the pivot. That reduces the torque.

The force stays the same distance from the pivot. It is not reduced. This applies to the middle axe, as well as the wheel example. No matter where you hold your hands on the handle (centered around the green line), the force from the imbalanced weight of the axe "pivots" around the green line. The green line is the axis through which the axe is being supported, regardless of hand position. The perpendicular distance from the Center Of Gravity to the green line does not change, no matter where on the handle it is supported.

If you still disagree, then please explain specifically how "you'd be reducing the distance of the force from the pivot", as you asserted for the wheel example.

 

[Goose 7279]

The axe that you made a handle for what i can see from the picture it appears that the haft would only balances the head if your holding it the way you are with hands where they are. Not where your hands would be after a slide or during the slide. If that makes sense. But there is alot i dont understand here so i may be out of my element.

 

[Woodcraft]

The axe that you made a handle for what i can see from the picture it appears that the haft would only balances the head if your holding it the way you are with hands where they are. Not where your hands would be after a slide or during the slide. If that makes sense. But there is alot i dont understand here so i may be out of my element.

You are exactly correct. You can pick up any single bit on a curved handle and see for yourself. Find the balance point for one finger and you can see how bit heavy the axe is or isn't. If you use two points of contact, one near the Apex of the big curve you can ",adjust" and find the easiest points to hold the axe like in the above pictures. If you move away from those points, (where you found it easiest to hold flat )on a bit heavy ax, it becomes harder and harder.
Try it, you can see quickly what is really happening. You are just using the curves of the handle to make it easier to hold the bit flat horizontally. If your hands leave those points, it becomes null and void for all horizontal purposes as far as this conversation is concerned.

This is a bit heavy ax. Plain and simple. Not that bad, but not perfect balance as you claimed 42.

 

[FortyTwoBlades]

The force stays the same distance from the pivot. It is not reduced. This applies to the middle axe, as well as the wheel example. No matter where you hold your hands on the handle (centered around the green line), the force from the imbalanced weight of the axe "pivots" around the green line. The green line is the axis through which the axe is being supported, regardless of hand position. The perpendicular distance from the Center Of Gravity to the green line does not change, no matter where on the handle it is supported.

If you still disagree, then please explain specifically how "you'd be reducing the distance of the force from the pivot", as you asserted for the wheel example.

The amount of force the handle experiences at point 1 remains the same as when your upper hand is at point 2, but your hand--when at point 2--experiences less torque than it was at point 1. When your hand is at point 3, point 2 on the handle is experiencing the same torque as it was before your hand was at point 3, but your hand is now experiencing less torque at point 3. Another way to think of it would be that the only reason why the head is torquing in the hands in the first place is because the handle is off-axis, and the less off axis it is the less torque you'll experience because the less mass and length is to that side of the handle. Well, as the hand moves down the handle, it's converging with the natural axle and so is less off-axis. Less of the mass of the tool is to that side of that hand, and so the amount of torque is reduced. Unlike the case of a wheel where you have fixed connective points, your hands are free to move in space rather than being affixed to a rigid body. However, an imbalanced wheel on the passenger side of a car is going to cause more vibration on that side of the car. The opposite side's fixed point of hold on the axle is closer to the center of gravity and so is less off-axis and subject to less torquing force.

 

[FortyTwoBlades]

The axe that you made a handle for what i can see from the picture it appears that the haft would only balances the head if your holding it the way you are with hands where they are. Not where your hands would be after a slide or during the slide. If that makes sense. But there is alot i dont understand here so i may be out of my element.

Nope. It balances with the hands at any point along the section below the offset neck. As my hand moves lower on the handle there's more desire for the whole head end to drop down, though, since I'd be farther from it, so it's a bit tougher to take a picture of it like that! But it's no more prone to rotate if held lower on that handle. Thankfully, it's a light axe so perhaps once it stops pouring outside I can take a few photos of it as proof. By contrast, I can't produce the same effect with the factory handle no matter where my fingers are positioned because the handle is off-axis.

Perhaps you're thinking that in the horizontal hold my upper hand is in the same spot on the handle as it was in the profile shot? 'Cause if so, it's lower by a bit, on the straight region.

 

[Woodcraft]

Nope. It balances with the hands at any point along the section below the offset neck. As my hand moves lower on the handle there's more desire for the whole head end to drop down, though, since I'd be farther from it, so it's a bit tougher to take a picture of it like that! But it's no more prone to rotate if held lower on that handle.

If that were true you should be able to do the test at several points on any thing like a wooden chair back, or a bar surface and if need be a dangling weighted line off the butt of the handle as a counterbalance if the head is too heavy. Go ahead an round out that flat and give it a try. (Of course if the ax was properly balance it would have a balance point near the head on the handle as well as bit to poll. We are talking about a tool that is swung horizontally. And if that were the case, you could prove the balance on one finger. Like a double bit.)

A really good example would for people to try is with a Hudson Bay pattern ax with a short curved handle. You will see how you can counter the heavy bit when the two points of contact are inside the curved zones. Once you go past these points, the bit drastically drops again. You can also do the same "trick" on a bit heavy Michigan on a curved 32" handle. Just drag it on a bar all the way to the bottom curve in the handle and find the point and "ta da" with a ton of counterbalance weight, presto, it is suddenly a balanced ax.

 

[Steve Tall]

The amount of force the handle experiences at point 1 remains the same as when your upper hand is at point 2, but your hand--when at point 2--experiences less torque than it was at point 1. When your hand is at point 3, point 2 on the handle is experiencing the same torque as it was before your hand was at point 3, but your hand is now experiencing less torque at point 3. Another way to think of it would be that the only reason why the head is torquing in the hands in the first place is because the handle is off-axis, and the less off axis it is the less torque you'll experience because the less mass and length is to that side of the handle. Well, as the hand moves down the handle, it's converging with the natural axle and so is less off-axis. Less of the mass of the tool is to that side of that hand, and so the amount of torque is reduced. Unlike the case of a wheel where you have fixed connective points, your hands are free to move in space rather than being affixed to a rigid body. However, an imbalanced wheel on the passenger side of a car is going to cause more vibration on that side of the car. The opposite side's fixed point of hold on the axle is closer to the center of gravity and so is less off-axis and subject to less torquing force.

I maintain that this is incorrect. The middle axe handle "experiences" a given (unchanging) torque resulting from the head imbalance being "countered" by the two hands supporting the handle, no matter where the two hands are supporting the handle along the green axis. As long as there are two hands holding the handle, the axis of support is the green line, and it does not get "less off-axis" with the natural "axle" as the hands move. The green line is at a consistent geometric angle with the red line, even at the point where the two lines converge.

An easy example:

The weight of the axe head plus handle is 6 pounds.
The Center of Gravity is 2 inches (measured perpendicular) from the green line.
The axe is held horizontally by two hands.
The resulting torque "experienced" by the handle (as well as total torque "experienced" by the hands) is equal to
6 pounds times 2/12 feet = 1 foot pound.

This 1 foot pound of torque is what the two hands (in combination) are providing, no matter where on the handle they are located. This 1 foot pound of torque does not diminish or go away, as long as the axe head is being held horizontally by two hands.