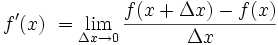Ideal and Real Geometry of Convex Edges

[Lagrangian]

I meant to post this in the "Degree of Sharpness" thread, but the server kept timing out, so I made a new thread. Moderators should probably move this post back into that thread?

I'm reluctant to get mired in various internet debates. ("Omg, someone is *wrong* on the internet!" https://xkcd.com/386/ )

But hopefully this is a succinct and clear explanation of what I believe *almost everyone* already knows, either intuitively or technically.

Let's separate our problem into two cases:
(1) The ideal mathematical case.
(2) The real world case.

You can see that if we zoom into the intersection of two smooth (ie: differentiable) curves, we form a "corner." If you were to zoom in infinitely close (infinite magnification), then the two sides of the corners will become the tangent lines. These two tangent lines intersect at the same point the two curves intersect.

"Differentiable" just means that if you zoom into a point on the curve then the curve gets closer and closer to the tangent line at that point. And as you take the limit of magnification going to infinity, the curve will become the tangent line (for an arbitrarily small neighborhood around the point of tangency).

The above is just informal; those of you who know calculus will be able to translate what I mean into technical math.

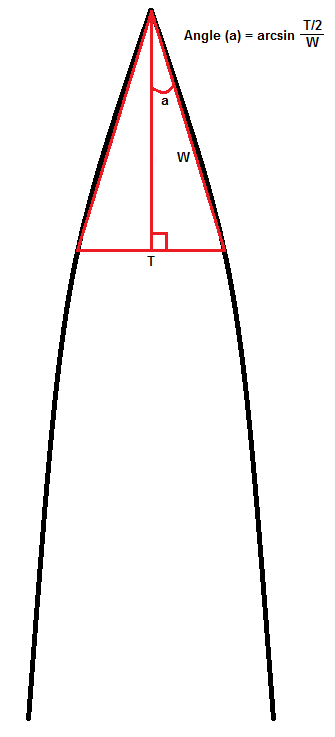
In the real world, the convex edge is similar to a v-edge. In the ideal mathematical world, both the V-edge and the convex edge have well defined angles at the apex. But we live in the real world, where *neither* v-edges nor convex edges have a "well defined" apex angle (at least not well-defined in the technical sense).

 

[Lagrangian]

Oh I forgot to mention that the diameter of curvature of the apex is labeled 0.1 microns, as suggested by measurements by forum member ToddS on his electron micrograph images.

 

[REK Knives]

I agree... we discussed this in another thread, here, which is an interesting read if you have time But the advantage to convex edges is that if you have the same apex angle, then you have pretty much the same lateral strength of the edge without having the shoulders of the edge to inhibit cutting ability.

 

[Obsessed with Edges]

I agree... we discussed this in another thread, here, which is an interesting read if you have time But the advantage to convex edges is that if you have the same apex angle, then you have pretty much the same lateral strength of the edge without having the shoulders of the edge to inhibit cutting ability.

That sums up my view entirely, on convexed grinds. I've never seen much (or any) advantage in taking a convex all the way to the true edge like some convexing purists might advocate, as it always results in dimimished cutting by making the apex geometry wider than if left alone. So long as the hard-edged shoulders of the previous V-bevels are smoothed out, the actual cutting geometry at the edge will be better off if it remains essentially a crisp 'V', even if that 'V' extends only a few microns behind the apex. My favorite & ideal 'convex' is one on which I've set an acute V-bevelled edge and made sure it's fully apexed and clean, and then applied the convex to essentially everthing BEHIND the apex, without altering the apex geometry at all. That always makes for great cutting, and has never let me down.


David

 

[Fred.Rowe]

The ideal would be a "V" edge with rounded shoulders, as is David's ideal, I agree.

The "V" edges I produce look much better than the representation of this "real" V edge. It's relative to the equipment used and skill level.

To make the comparison equal, the "V" edge should be equal to the dimension across the shoulders. or the convex edge could be expanded to equal the same dimension.
If the claim is " the rounded shoulder are more efficient or pass through the material easier, with a convex edge, make them equal. If you do the "'V" will be sharper as well as thinner. Apples and bicycles will not do

Fred
'

 

[HeavyHanded]

Oh no...

No one makes a convex that arcs all the way to the end, there's a different name for that sort of edge, called "botching the job". The word "convex" in this case may be a misnomer as it applies to the shape of the transition between two planes, and not the edge itself.

If one sits and ponders, neither can claim to be thinner. As long as there are two planes that intersect, they can be joined by an arc that will reduce the area without changing the angle.

And one can then join two points at either end of the arc to make a space with smaller area...

That can be bridged by an arc to make a smaller yet area...

That can be joined at the extremities by a straight line to make an even smaller area...

That can be....

Until both are a straight line.

 

[Fred.Rowe]

Martin,


As a person that does sharpening, think of it this way. An individual comes into your shop with a piece of flat stock with 1/8" spine, 1 1/4" wide. They ask you to put a convex edge on it that is 45* at the apex - this is critical, it cannot go less than 45* at the edge, 22.5" on either side. They don't want an angled primary grind, just convex it into the apex.

They leave and you get to work. You make short work of it. They call back and say they changed their mind after reading this thread, and now want a V bevel but still 45* apex with flat sided primary and keep it at 1 1/4" from cutting edge to spine. Without shrinking the spine to apex dimension, or making a steeper primary grind, it cannot be done - the material that would have made up the shoulders is already gone - doesn't matter what the shape of the arc is that forms the convex, as long as it finished at 45*.

My response would be "call Martin"

With this same scenario but changing one thing, the width of the shoulders cannot be changed as well as the height of the blade. At Martin's shop, a convex edge is ground within these parameters, the man calls back, changing his mind wanting a flat edge at the same angle, same shoulder width, Martin grinds the flat edge, no problem, [patience of a saint I must point out].
If you reverse the story and the man starts with the V edge and then wants it changed to a convex edge, maintaining the geometry, it can't be done.

Fred

 

[HeavyHanded]

Martin,


As a person that does sharpening, think of it this way. An individual comes into your shop with a piece of flat stock with 1/8" spine, 1 1/4" wide. They ask you to put a convex edge on it that is 45* at the apex - this is critical, it cannot go less than 45* at the edge, 22.5" on either side. They don't want an angled primary grind, just convex it into the apex.

They leave and you get to work. You make short work of it. They call back and say they changed their mind after reading this thread, and now want a V bevel but still 45* apex with flat sided primary and keep it at 1 1/4" from cutting edge to spine. Without shrinking the spine to apex dimension, or making a steeper primary grind, it cannot be done - the material that would have made up the shoulders is already gone - doesn't matter what the shape of the arc is that forms the convex, as long as it finished at 45*.

My response would be "call Martin"

With this same scenario but changing one thing, the width of the shoulders cannot be changed as well as the height of the blade. At Martin's shop, a convex edge is ground within these parameters, the man calls back, changing his mind wanting a flat edge at the same angle, same shoulder width, Martin grinds the flat edge, no problem, [patience of a saint I must point out].
If you reverse the story and the man starts with the V edge and then wants it changed to a convex edge, maintaining the geometry, it can't be done.

Fred

Hah hah,
I give him my best Scottie impersonation and say "I'm given er all she's got Cap'n, but if I do that she's gonna BLOW!"

Or I just grind the primary in a little bit and hand it back with a straight face. Building it up with Bondo and metallic spray paint or silver solder might also be on the table, this guy's probably never going to use it anyway.

 

[Fred.Rowe]

Hah hah,
I give him my best Scottie impersonation and say "I'm given er all she's got Cap'n, but if I do that she's gonna BLOW!"

Or I just grind the primary in a little bit and hand it back with a straight face. Building it up with Bondo and metallic spray paint or silver solder might also be on the table, this guy's probably never going to use it anyway.

A little play acting is called for under certain, extreme conditions. ha ha

 

[chiral.grolim]

*sigh*

I commented in the previous thread, but apparently it is still not clear to folk:

...As long as there are two planes that intersect, they can be joined by an arc that will reduce the area without changing the angle...

This is utterly and immutably WRONG.
For starters, an arc is a curved plane, in 2D it is a curved line. If any two points (A & B) along that arc are joined by the shortest length possible - a straight 'secant' line - then an arc lying "above" that line (or thicker) is called "convex" and an arc lying "below" that line (or thinner) is called "concave" or "hollow". Those are the meanings of the words. Get that straight. (pun intended)

If you have a meeting of two flat planes and curve an arc beneath them, that arc has a beginning and an end (apex and bevel-shoulder in this case) and beneath that arc (for convex), the shortest possible secant drawn to join those two points or any other two points along that curve is a flat line (or plane). You cannot "reduce the area" further than that flat line without creating a concave arc beneath it. There is no "chase" that can occur unless you keep running the bevel height higher and higher or thin the spine of the knife itself, thus changing the geometry utterly. It should be obvious to HH that even in his "chase" scenario the final bevel is what? A flat line.

Second, as previously stated but here now again, a curve cannot be used to form a measurable angle - it is not possible. An "angle" is the space between flat lines. To present any sort of angle for a curve, you must derive that angle from a straight line drawn between points lying on that curve - a secant - which in the case of a "convex" curve must, by definition, lay beneath that curve = thinner.

 

[chiral.grolim]

Let's separate our problem into two cases:
(1) The ideal mathematical case.
(2) The real world case.

...

You can see that if we zoom into the intersection of two smooth (ie: differentiable) curves, we form a "corner." If you were to zoom in infinitely close (infinite magnification), then the two sides of the corners will become the tangent lines. These two tangent lines intersect at the same point the two curves intersect.

"Differentiable" just means that if you zoom into a point on the curve then the curve gets closer and closer to the tangent line at that point. And as you take the limit of magnification going to infinity, the curve will become the tangent line (for an arbitrarily small neighborhood around the point of tangency).

Absolutely incorrect.

The concept of "tangent" is ethereal, imaginary, it does not exist in reality. Again, the equation to derive a tangent from a curve:

The equation requires knowledge of the function defining that curve. In our real-world situation, you will never have that, but let's ignore that key fact for now. The delta-X is the measurable length of a flat line connecting two points (A & B) along the curve, and again, by definition such a line must fall beneath (i.e. thinner than) the "convex" curve. The "tangent" is the theoretical line you would draw between A & B if A=B... except that when A=B you cannot draw any line as there is no length, no distance, between them, they are identical. Note what happens to the equation if delta-X = 0, division by 0! It is a mathematical impossibility, "tangent" is a concept NOT a reality. INSTEAD the value given for "tangent" is in fact that of some secant where A does NOT equal B but the length is sufficiently small for the intended use, and that can be really really small. The curve will never "become the tangent line", that is the precisely WRONG way to think about it, it is backwards. The correct way to understand it is that, upon "infinite magnification" there are smaller and smaller flat secant lines that can be drawn between points on the curve (the "arbitrarily small neighborhood), and it is these lines that provide the slope for an angle measurement, and again the lines are, by definition, beneath the curve if it is "convex".

In the case of Gillette and ToddS, each provide the level of magnification they are willing to achieve to provide measurements of those secant lines, and it is from those and those alone that an angle can be derived. And how is that angle calculated? I'm glad you asked! Like this:

Are y'all sick of that image yet? To help HH, understand that the 'T' and the 'W' are as small as can possibly be measured, and also as large as is practical to bother measuring.

"Differentiable" means that for all values of the function (a curve in our case, but you must already know the equation of that function!) the tangent can be derived per the above equation, i.e. using secant lines.

What i hope to achieve is the understanding that, in the real world or the ideal math world, the only difference is the level of magnification possible. In BOTH situations, "convex" is thicker (lies outside or above) "flat", it MUST or finding a derivative is impossible. The "terminal" or "working edge angle" must and is always defined by flat lines as shown in the image I presented.

 

[chiral.grolim]

In the real world, the convex edge is similar to a v-edge. In the ideal mathematical world, both the V-edge and the convex edge have well defined angles at the apex. But we live in the real world, where *neither* v-edges nor convex edges have a "well defined" apex angle (at least not well-defined in the technical sense).

Again, the bolded above is wrong in the sense you describe it. "Convex" describes an arc which has no defined angle outside of using flat lines lying within the arc to describe it. That is the best you can do with a convex edge. It is also, by the way, the best you can do with a concave edge, only in such a case the flat line is necessarily above or thicker than the curve.
But yes, in the real world as I've mentioned many times before, the edge is rounded over.


As to the purpose of using a convex edge, I think it is described well in the Gillette patent previously cited:

...provides a blade tip having a wider forward profile near the blade tip ... while maintaining a narrow profile away from the blade tip...

The convex curves back from the apex in such fashion that it maintains a thicker tip-section than would be provided by a flat-grind of the same height and thickness, with a gradual bevel-transition into the primary (no distinct bevel shoulders to act as stress points). An increases the number of bevel-planes and by so doing increases the angle adjoining those planes.

Geometric honesty: Whatever the height and thickness of your bevel, THAT is THE height and thickness of your bevel.

EDIT TO ADD: in the above butchered image, the "ideal convex" is not "convex" relative to the V bevels it thins out, it is only "convex" relative to the red lines I depicted in my revision of the "ideal V edge", which also serves to derive the "working" or "terminal" angle of the convex edge. The convex edge does NOT share the angle of the grayed V bevel.

 

[Lagrangian]

Not sure how to respond; we may have different understandings of what is a mathematical limit.

Mine is simply based on conventional analysis and calculus as taught in undergraduate math at a top 10 university in the US. It's what you find in standard mathematical analysis books.

Let's consider the standard Newton definition of derivative.

One might argue that this equation makes no sense, because if we plug in delta X = 0, then we are dividing zero by zero. However, that is not what we are actually doing in mathematics. We are taking a *limit* as delta X goes to zero. This limiting process is well defined, but is rather technical. In a forum like this, I doubt it is worth reviewing the foundations of modern calculus.

Rather than getting bogged down in either trying to explain basic analysis, or maybe trying to convince readers that I understand basic undergraduate analysis, I'll just point out some textbooks used in the courses I took. Perhaps you disagree with the current convention of how calculus and analysis are defined; if so your argument shouldn't be with me, but with standard textbooks.

http://www.amazon.com/Vector-Calcul...id=1430258940&sr=8-1&keywords=vector+calculus
http://www.amazon.com/Mathematical-...d=1430258961&sr=8-1&keywords=analysis+apostol
http://www.amazon.com/Principles-Ma...qid=1430258975&sr=8-2&keywords=analysis+rudin
http://www.amazon.com/Introductory-...0&sr=8-5&keywords=applied+functional+analysis
http://www.amazon.com/gp/product/04...rd_t=36701&pf_rd_p=1970566782&pf_rd_i=desktop

To simplify the discussion it is worth separating the ideal mathematics from the real-world. When you get down to it, it is all atoms. You might not think that matters, but modern diamond knives have an apex which is roughly 5 nanometers wide. That is roughly the diameter of 15 carbon atoms. For those who are curious, more details in the links below.
http://www.tedpella.com/diamond_html/diamondk.htm
http://en.wikipedia.org/wiki/Van_der_Waals_radius

I think that we agree on what is happening in the real world. We've all seen the electron micrographs from John Verhoeven, ToddS, etc. So that is fine.

I think we disagree on how the mathematics is defined. That's fine too. Just keep in mind that I am simply reflecting what is understood in conventional calculus and analysis, based on basic point-set topology and the epsilon-delta definitions of limits (as described in the textbooks above).

 

[HeavyHanded]

*sigh*


This is utterly and immutably WRONG....
For starters, an arc is a curved plane, in 2D it is a curved line. If any two points (A & B) along that arc are joined by the shortest length possible - a straight 'secant' line - then an arc lying "above" that line (or thicker) is called "convex" and an arc lying "below" that line (or thinner) is called "concave" or "hollow". Those are the meanings of the words. Get that straight. (pun intended)

If you have a meeting of two flat planes and curve an arc beneath them, that arc has a beginning and an end (apex and bevel-shoulder in this case) and beneath that arc (for convex), the shortest possible secant drawn to join those two points or any other two points along that curve is a flat line (or plane). You cannot "reduce the area" further than that flat line without creating a concave arc beneath it. There is no "chase" that can occur unless you keep running the bevel height higher and higher or thin the spine of the knife itself, thus changing the geometry utterly. It should be obvious to HH that even in his "chase" scenario the final bevel is what? A flat line.

*Facepalm*

The final "bevel" is no longer a bevel or an arc, it is a flat line that no longer describes the original angle anywhere along its length - no angle, no bevel. That is the final elimination of relationship to the original theoretical apex angle that was our constant.

Bevel:

the angle that one surface or line makes with another when they are not at right angles

I honestly have no idea what you are carrying on here. I have referenced a simple diagram that describes a series of curved lines and two lines joined by an angle. Both series repeatedly follow the same path to the same straight final line and make an angle with the same value in degrees. It doesn't get any more simple than that. And it gets even easier, as the tangent isn't entirely theoretical, it extends out from the arc along a straight line that can easily be measured.

You are asking me to believe you and your fuzzy application of geometry over my lying eyes - its right there to look at and in a manner that is easily reproduced in the real world on a three dimensional object. Also, you will note that every instance as it progresses down, the V bevel must reduce the primary grind to keep pace - the "convex" at any given intersection of primary and cutting bevel has less mass behind the edge. The V bevel can undercut it, but will need to thin the primary to get it done, as I've been saying all along. To undercut the arc, the V bevel must trade some degrees from the spine and give to the cutting bevel shoulder to maintain 360° total. There's a simple reason for this. Once you start replacing an intersection of straight lines in a geometric figure for an arc that approximates the same angle, the resulting space will have less area. Back to the whole concept of a "shortcut".

Feel free to blow this diagram up for a better look. Also feel free to mark it up if needed to advance your point.

If the phrase "convex" doesn't apply here so be it, but the concept as I am applying it is right there to see and is how anyone who understands "convex" edges is going to apply it when they craft their edges. Or if they don't they should start!

Here is an interesting experiment. Below is a diagram showing four geometric figures. The area bounded by the green and black lines on two sides, on the other two sides we have two straight lines joined at a point, a fixed angle, to meet another angle on the lower right. The second set of figures shares the right and upper lines but incorporates an arced line in place of the two straight lines.

Again, we have a constant in that both figures total 360°, yet the region joined by the arced line has less total length and less surface area in both cases than the two planes joined by an intersection of straight lines. Applied to a 3D structure that equals less mass.

 

[bpeezer]

Hey chiral.grolim, if we call it a "curvilinear" bevel instead of a "convex" bevel, will you be content?

 

[Fred.Rowe]

Hey chiral.grolim, if we call it a "curvilinear" bevel instead of a "convex" bevel, will you be content?

:thumbup::thumbup:

 

[Lagrangian]

I'm simply explaining the conventional definition in mathematics. It's the same as described in Wikipedia. It is a rather mundane and ordinary definition, so I think there shouldn't be any controversy.

"Angles between curves

"The angle between the two curves at P is defined as the angle between the tangents A and B at P
"The angle between a line and a curve (mixed angle) or between two intersecting curves (curvilinear angle) is defined to be the angle between the tangents at the point of intersection."

http://en.wikipedia.org/wiki/Angle#Angles_between_curves

 

[Pondoro2310]

I took a lot of Calculus many years ago and also taught high school math for a few years. I agree with Lagrangian's definitions. I'm not sure it helps sharpen knives much but his math is correct. Since this part of the forum is for maintenance, tinkering, and embellishment I think his post is appropriate.

 

[chiral.grolim]

I'm simply explaining the conventional definition in mathematics. It's the same as described in Wikipedia. It is a rather mundane and ordinary definition, so I think there shouldn't be any controversy.

"Angles between curves

"The angle between the two curves at P is defined as the angle between the tangents A and B at P
"The angle between a line and a curve (mixed angle) or between two intersecting curves (curvilinear angle) is defined to be the angle between the tangents at the point of intersection."

http://en.wikipedia.org/wiki/Angle#Angles_between_curves

Yes, and how is that definition arrived at? You must first understand THAT to understand the math.

Not sure how to respond; we may have different understandings of what is a mathematical limit.

Mine is simply based on conventional analysis and calculus as taught in undergraduate math at a top 10 university in the US. It's what you find in standard mathematical analysis books.

Let's consider the standard Newton definition of derivative.

One might argue that this equation makes no sense, because if we plug in delta X = 0, then we are dividing zero by zero. However, that is not what we are actually doing in mathematics. We are taking a *limit* as delta X goes to zero. This limiting process is well defined, but is rather technical. In a forum like this, I doubt it is worth reviewing the foundations of modern calculus.

Actually, it may be necessary to help clarify for folk what I am explaining. The equation makes perfect sense, but first one must recognize some of the parts for what they are.
For example, what is delta-X? It is a secant-line, a straight (flat) line connecting two points on the curve and in the case of a "convex" curve it necessarily falls beneath the other points on the curve. ONLY a curve ABOVE that secant line can be defined as "convex". Understand the definition of "convex"?
Second, the equation defines the tangent of the function (our curve) at a point X to be the line NOT at point X - as a point cannot be used to define ANY line, a line requires two points - but rather at the secant-line of smallest length between point X and some point Y (I've been using A & B, but it makes no difference) such that the length between them is a flat line with length delta-X. IF the tangent line WERE confined to point X, you would not have a line, indeed what you would have is delta-X = 0, which leads to division by 0.
Is this clear? In a "limit", you can never actually reach the value, you can only approximate it, and that approximation IS the output value! To help:
http://en.wikipedia.org/wiki/Limit_(mathematics)

Suppose f is a real-valued function and c is a real number. The expression

means that f(x) can be made to be as close to L as desired by making x sufficiently close to c. In that case, the above equation can be read as "the limit of f of x, as x approaches c, is L".

A curve HAS no ability to form an angle... but straight lines do! So we "define" the angle of a curve as what? The closest approximation desired through the use of secant lines. "Tangent" is theoretical, it is a line perpendicular to the radius of a curve and intersecting the curve at only a single point. But since a single point cannot EVER determine a line, the tangent must be arrived at some other way. One way is through a derivative - IF you know the equation of the function for the curve (which, as previously stated, we never do, we just use computer modelling to extrapolate a "best fit"), you can take the derivative which gives you what? A "limit" value, i.e. an approximation. Alternatively, if you know the equation of the function and can generate a perfect circle to fit within the curve (again, requires computer modelling to create a "best guess" approximation) you can generate a radius of the curve against which the tangent can intersect at exactly 90-degrees. No matter what you do, the slope of the tangent and any angle derived therefrom is an approximation made using an arbitrarily small length of secant line connecting points on the curve, and a "convex" curve to which it corresponds MUST, by definition, fall above that line = thicker. Always.


So again, the image I presented of T and W with angle (a) is the way it is done. 'W' is the secant line of arbitrary length delta-X, T is the thickness corresponding to length 'W', and (a) is the angle generated from the slope of length 'W'.

Again, the problem y'all seem to be having is the idea that tangent lines are a physical reality. Understand, they are not even a mathematical reality in the sense you describe. A tangent is like an asymptote, the flat line the curve approximates but never actually reaches. The defined slope of a tangent is in reality the slope of a secant-line really close to the point you want that line confined to, but since you cannot define any line with a single point you have to make due with what you have available to you.

(a gif i pulled from the web)

THAT is the math. I would LOVE to hear someone else's understanding of "limit" and also "tangent" and even "convex" that defies these principles which ultimately rely upon the impossibility of division by zero. What you are suggesting is exactly that, that we should divide by zero to get the angle of the convex edge, in which case the angle can be ANYTHING because you just threw the math out the window.

Furthermore, i don't get why y'all are so focused on "tangents" when they only describe a single point without ANY thickness or length, i.e. utterly in-applicable to ANY bevel which MUST HAVE LENGTH. What's with that??? Not only does it not make sense in MATH, it doesn't make sense in the physical world!!

...To undercut the arc, the V bevel must trade some degrees...

That is not how it works, and AGAIN the arc is ONLY "convex" in relation to the flat beneath it. Do you really not accept the definition of the word "convex"??? Because that is what this seems like...

 

[samuraistuart]

Wow, my spider webbed filled head is spinning! I admit that convex edges are a bit foreign to me. I've read about them, quite a bit, but never have made one or even played with one. I found something very interesting here in these posts that helps clear things up a bit for me. The convex never really goes all the way to the edge apex. Is that right? If so....that makes a LOT of sense to me now. This whole time I'm thinking to myself, "how are these guys able to produce a sharp edge that has radius all the way to apex?" I think maybe there are some guys that can do exactly that, but to me it makes more sense to have a radius that essentially "knocks off" the shoulders of a V grind edge!

And that is exactly what I do in my production knives, sort of. Starting with a blade that has been heat treated and NOT polished, and an edge that is, lets say .010" thick, I sharpen it to just about apexing. Then I go back and "knock off" those shoulders and at this point as I polish the entire blade. Essentially my apex is a microbevel applied to a curved edge. Wow do they glide thru stuff!