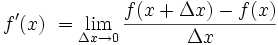Ideal and Real Geometry of Convex Edges

[chiral.grolim]

One more post that might help or make things worse:

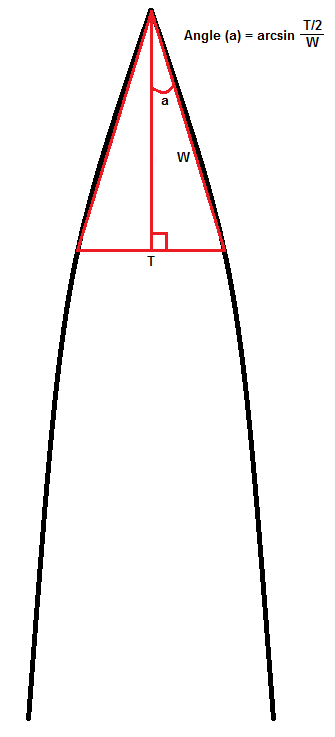
You present to me a blade with convex edge (curved all the way to the apex), and then you tell me that the apex angle is between the intersection of the tangents to the curves, and that said is angle is X, and the curve falls beneath the tangent line at every point except the intersection (i.e. it is thinner). Here is what I will ask you:

First, how did you derive the tangents of each curve? You'd need the equation of each curve to do that, and not just an approximation given by a "best fit" computer analysis from data points generated by measuring thicknesses and distances back from the apex, also taking into account the limits of the precision of those measurements. To wit, you DO NOT know the the slope of any tangents on your curve, you approximated it based on a computer model that used secant lines and mathematical limits to derive that value.
Second, you do know that "convex" relates only to curves ABOVE an associated flat line (i.e. thicker), don't you? As such, your curve is not "convex" relative to the tangent lines, so why are you describing it that way??
Third, what relevance would finding a tangent to a curve have in relation to cutting performance of said curve since that angle is only representative of a single dimensionless point? Cutting is a physical process that involves inserting a bevel with physical dimensions into a cutting medium that also has physical dimensions, with cutting-depth and lateral strength being of rather key importance, i.e. the bevel angle needs to be relevant for some length >0, which is not the case for a tangent. So... why did you bring it up??

*shrug* just some thoughts.

I agree with samuraistuart and those that have presented "convex" as a technique smoothing down the shoulders between bevels back form the edge, though I suspect many strop the very apex which adds micro-convexity to the edge as well.

 

[Fred.Rowe]

I agree with samuraistuart and those that have presented "convex" as a technique smoothing down the shoulders between bevels back form the edge, though I suspect many strop the very apex which adds micro-convexity to the edge as well.

Convex edges are two distinctly different geometries depending on the process. Most people posting on this tread, I believe, is expressed in the form of a flat apex, in the form of a "V" with the area behind the "V" being rounded or convex. The shoulders are rounded over, the idea, to improve penetration when cutting.
A person that grinds a convex edge on a belt machine is closer to true convex, in that, the edge is produced by pressing the edge into a moving belt where the depressed belt "rounds" the entire edge assembly apex through shoulders.
The convex edges created on a flat stone or plate are quite viable because the cutting edge is flat and efficient, whereas the one done on a depressed belt leaves a lot to be desired.

To me the belt edge is pretty amateurish, the edge does not perform at optimum inside a comparable geometry, its the least efficient of the three. Flat, flat with rounded shoulders, and true convex, ground on a moving belt.

Fred

 

[Twindog]

To my thinking, the most important aspect of generalized cutting performance is the width of the edge shoulders. Second would be the angle of the edge. When these two aspects of blade/edge geometry are optimized, I suspect that there is little to no advantage in rounding off the shoulders.

Where rounded shoulders on a V edge work best are where the blade/edge geometry is fairly obtuse. And even there, you can cut a flat bevel into the shoulder that will work just as well as rounding. Or you could go with a steeper back bevel and add a micro-bevel.

When I went in for my eye examination a couple weeks ago, the doctor had a new whiz-bang scanner that detailed the topography of my retina with unbelievable precision and detail. It occurred to me later that this technology would be interesting to scan edge profiles to see what the micro-geometry profiles our edge bevels actually look like. My guess is that most people would be surprised to see what kind of edge they have created.

 

[Fred.Rowe]

To my thinking, the most important aspect of generalized cutting performance is the width of the edge shoulders. Second would be the angle of the edge. When these two aspects of blade/edge geometry are optimized, I suspect that there is little to no advantage in rounding off the shoulders.

Where rounded shoulders on a V edge work best are where the blade/edge geometry is fairly obtuse. And even there, you can cut a flat bevel into the shoulder that will work just as well as rounding. Or you could go with a steeper back bevel and add a micro-bevel.

When I went in for my eye examination a couple weeks ago, the doctor had a new whiz-bang scanner that detailed the topography of my retina with unbelievable precision and detail. It occurred to me later that this technology would be interesting to scan edge profiles to see what the micro-geometry profiles our edge bevels actually look like. My guess is that most people would be surprised to see what kind of edge they have created.

Agreed, if the knife is built correctly from the spine down, with the proper primary bevels and the edge taken to as close to zero as possible, there are many options at the edge. I'm finishing up a set of W2 kitchen knives that are .089 at the spine with a 2 degree primary bevel, the edge taken to zero before sharpening. I keep the edges taped even before the edge is ground in. I'm going with a "V".

 

[Lagrangian]

Hi chiral.gromlin,

Just a few points:

(1) I think you would like the modern mathematician N. J. Wildberger. He believes there are problems or rather "unresolved" issues with modern calculus. You can find him on YouTube. Here is a lecture of his that gives an overview of what he thinks are some problems with modern calculus. I think you will really like this.
https://www.youtube.com/watch?v=fCZ8jJCVinU

(2) I'm just reflecting what conventional mathematicians, scientists, and engineers think and do. If you disagree, that's fine. It just means you think conventional math is flawed, like Prof. Wildberger. I think there is some truth to what Wildberger says, but I mostly agree with the conventional perspective in mathematics.

(3) In conventional math, we are okay with saying we have some abstract function f(x) that is differentiable, and studying f(x) even if we can't write the equation for it. Mathematicians often talk about and proven theorems describing the tangent lines of f(x) even though they don't know f(x) well enough to write down an equation for it. Perhaps in the future, mathematicians will invent a way to write some f(x) as an equation. Sometimes mathematicians will say, the derivative and tangent lines of f(x) exist, but we just don't know what they are. Or if the tangent lines do not exist at a certain point on f(x), then mathematicians prove that f(x) is not differentiable at that point. If there is a "corner" at x0 in f(x), there are rigorous definitions of "left derivative" and "right derivative" where left and right mean you take limits approaching from the left and right sides of x0. This is simply a jump discontinuity in the derivative, f'(x) at x0. The height of the jump is a measure of the corner's angle (really, just an instantaneous change in slope, and one can convert slopes to degrees using trigonometry, such as the arctangent).

(4) If you want to communicate with the vast majority of scientists, engineers, and mathematicians, then it's good to know conventional math (even if you think it is flawed). Otherwise, it can be difficult to get your point across.

(5) I don't think our disagreements really matter. Perhaps we disagree about what it means for a tangent line to exist, or what a limit is, or when something is mathematically well defined. But that's okay. We understand each other. I believe you've explained yourself clearly, and I would like to think I have been clear too. If we share some respect, I think that's all that matters.

Sincerely,
--Lagrangian

 

[chiral.grolim]

Lagrangian,
I appreciate your reflections, which is why I continue to post on this subject. Nothing I have posted is in any way controversial among mathematicians or contradicts convention, nor do I consider any of the issues here presented "unresolved". It is important that I explain this once again given your declaration of your education on the matter and your appeal to authority.

(part 1, since BF keeps resetting my connection)

 

[samuraistuart]

Fred, the W2 kitchen knives ground like that would be light sabers. Now if you could only figure out a way to make the edge glow "green", "blue", or "red", and get it to make the sound a light saber makes when swinging thru the air!!!

We do similiar.....

Most all my knives....starting with an edge that is flat ground from spine to almost zero (barely reflecting light), sharpening a V edge on that (whatever angle you want....say 12 per side just for kicks), and then rounding off the shoulders that were created! You end up with an incredibly thin edge that has a tear drop or apple seed shape to it. No stropping done in my shop. If a super polish edge is needed, 12K waterstone no slurry.

Now if the knife is the type that might see some wood carving or more serious work, then starting with a thicker edge before sharpening, say .010" or even .020" might be warranted.

Good thoughts guys. I am learning stuff in this thread! Even amongst the technical jargon! Good attitudes too!

 

[chiral.grolim]

We define the angle at the intersection of two curves how? Curves cannot create an angle, only flat lines can do that, it is corollary to the impossibility of division by zero as I showed above. But we still want a way to describe the point of intersection, thus the concept of "tangent" - a line that just "touches" the curve, applicable at a single point only. But a single point cannot create a line, moreover it is dimensionless and so cannot create an angle, that is ALSO a corollary of the impossibility of division by zero as I showed above.
Nevertheless the line exists conceptually, so we derive it through limits using secant lines. It must be understood that the limit value is only conceptual - it is never reached, it does not exist even in the "ideal math" scenario, just like 1/(infinity) is NOT zero nor any other value, it is a concept. The difference in regard to tangents to a curve is that the value of the slope of the tangent IS real, but it cannot be reached in the way you and others have been describing, which is the way the slope is conventionally derived, nor should it be. And there is nothing wrong with that. But the secant lines DO exist, the slope value can be reached, calculated, measured, etc. A secant is a line that is more than just conceptual, and the intersection of secant lines DOES form an angle. And that is why, even in the "ideal math" scenario, secant lines determine the angle of intersection between two curves, secant lines produce the tangent conceptualized.

An alternative means to achieving the "real" slope of the conceptual tangent is indeed taking limits from both the left and right of the point in question, and then using a secant line that 'bridges' the point of interest, i.e. the line between points A & C that does not intersect point B and is parallel to a line that intersects point B but not A & C. Does this make sense?

What I have been straining to make clear, and I apologize if my poor teaching ability has failed for many minds, is that trying to use "tangent" as if it were anything more than a concept to describe the geometry at the apex of a convex edge is utterly and immutably wrong BOTH in the "ideal math" scenario AND in physical reality.

As i have worked to make clear, the "tangent" value is only conceptual in the math scenario, its value is theoretical and does not actually exist. Moreover, even if the value DID exist in the "ideal math" scenario, it would only be applicable at a single point without measurable impact on any of the surrounding points because a single point is utterly dimensionless. As such, it is utterly inapplicable to a scenario regarding geometry of a BEVEL on a knife blade (i.e. the rest of the curve). Finally, the tangent is only able to be derived IF the function defining each curve is known. In the "ideal math" scenario, if you don't have those functions, you cannot derive ANY value for the tangent, conceptual or otherwise. If you have a limited set of data points, you can generate a "best guess" equation so fit those points and serve as an approximate function from which you can derive a conceptual tangent, but WHY?? It is already irrelevant, you're simply adding GREATER margin for error by inventing a function to approximately fit the data points on the curve so that you can then take a limit to approximate the value of the slope of the tangent at a single point on that curve. You wasted your time.

In the "physical reality" scenario, the "ideal math" concepts still apply, i.e. "tangent" is still inapplicable only more so due to the reality of constraints on precise measurement AND the reality of constraints on the achievable dimensions of physical objects.
In the real world, there is no "single point" to define the apex meeting of two curves, rather it rounds over into a single curve which can at best be described as flat at the apex.
Let's say you ignore that reality and pretend that the apex does form a point - well, in order to derive a tangent of the curves to that point, you need a function to describe each curve, and you don't have that, so you must approximate, which is no small task. You do it anyway but the tangents you generate only intersect the curves at that single pretend apex point which is not applicable to the geometry of the bevel since a bevel must have measurable length/width and a point doesn't have that, nor does a tangent - a tangent only has slope and position. And the reality of tangents is that they are only approximations anyway, so your approximation of an angle doesn't actually apply to anything in reality. Why did you do it, again?
Finally, the entire point was to describe the geometry of a "convex" edge, and the very definition of the word "convex" demands that any flat line to which it be compared fall beneath that curve, which the pretend tangent (which took extraordinary efforts of imagination to arrive at) does not, so the curved bevel cannot even be called "convex" in relation to it. Failure at every turn. But it is GOOD that you failed because the entire effort was predicated on division by zero.

In the "ideal math" scenario, the geometry is characterized by taking secant lines to a mathematical limit and THAT is how the angle of intersection of the curves is arrived at, THAT is how it is characterized.
In the "physical reality" scenario, the geometry is characterized by taking secant lines to a physically measurable limit and THAT is how the angle of intersection of the curves is arrived at, THAT is how it is characterized.

Once more, how it is done:

***In BOTH scenarios, those secant lines fall beneath the "convex" curve by definition, i.e. the corresponding flat geometry is ALWAYS necessarily thinner AND that thinner geometry IS how the "terminal angle" is described.***

Is this the hard part for folk to understand? That the convex curve can be characterized with the same angle but be thicker than the corresponding flat geometry? Understand the conceptually the shortest secant line used to describe the angle of the curvature is defined by two adjacent points, i.e. non-identical points whose unique positions are indistinguishable, meaning the distance between them can be characterized as 1/(infinity) - not zero (because then they would be identical and you could not have a line) but nearly so. In reality, we can only measure with limited precision, so the best secant line to characterize the angle of the curve is the smallest measurable line, which is what 'W' in my chart represents, i.e. it is the best characterization able to be achieved. The physical object can be measured and the angle calculated, and the angle is applicable to a physical bevel - no "best fit" approximations of functions to describe the curvature, no limit-approximations of a tangent that is only applicable at an immeasurably small single point that only exists conceptually and certainly cannot be applied to a bevel, and no contradiction of the term "convex"!

Does anyone have ANY argument, from math or reality, that can explain why anyone would use "tangent" in this scenario in defiance of the mathematical tools required to approximate the tangent and without regard for the method (i.e. secant limits) use to achieve that approximation, as well as in defiance of the very definition of the word "convex"?? THAT is what boggles my mind. STOP saying "convex is thinner than flat" - by the "conventional" definition of those words, the statement is utter nonsense.


Thank you for your time.

 

[bpeezer]

Lagrangian,
I appreciate your reflections, which is why I continue to post on this subject. Nothing I have posted is in any way controversial among mathematicians or contradicts convention, nor do I consider any of the issues here presented "unresolved". It is important that I explain this once again given your declaration of your education on the matter and your appeal to authority.

(part 1, since BF keeps resetting my connection)

What you are saying contradicts sound calculus. I see that as fairly controversial.

 

[ToddS]

What you are saying contradicts sound calculus. I see that as fairly controversial.

I read the post fairly carefully and I don't see anything that contradicts my understanding of calculus. I admit that I haven't done much high level calculus since I was in graduate school, but these seem like undergraduate-level concepts to me.

Can you be more specific about where the contradictions are?

 

[bpeezer]

I read the post fairly carefully and I don't see anything that contradicts my understanding of calculus. I admit that I haven't done much high level calculus since I was in graduate school, but these seem like undergraduate-level concepts to me.

Can you be more specific about where the contradictions are?

The assumption that the definition of a derivative necessitates a division by zero, and thus is merely an approximation. Differentiable curves can have well-defined, accurate derivatives that will describe the tangent slope at any point along the curve.

 

[chiral.grolim]

The assumption that the definition of a derivative necessitates a division by zero, and thus is merely an approximation. Differentiable curves can have well-defined, accurate derivatives that will describe the tangent slope at any point along the curve.

(chiral proceeds to steel images from the web)

The definition of a derivative:

The notation "Lim" over "h -> 0" indicates that the output value is derived via approximation. Why the need to approximate? Because at h=0, you have division by zero. Approximating to avoid division by zero is part of the definition. That isn't controversial, is it?

EDIT to add:

Again, the equation to derive the tangent of a curve:

What is delta-X? It is some (measurable, value-associated, direct) distance between 2 points. A line is defined by two points. If delta-x is zero, then there is not two points, there is only one point which is not enough to define a line and the equation ends up with division by zero. Delta-X cannot be zero, it can only approximate it.

Further Edit: an approximation is a description, and "tangent" describes (via approximation) the changing slope of a curve, but it does so conceptually as applied to a single dimensionless point which is not relevant, and the line it generates eliminates the ability to describe the corresponding curve as "convex".
We wish to describe the "terminal angle" of a "convex" bevel. What is a bevel? A sloping surface, a line, a measurable, value associated distance between two points, i.e. delta-X. Well, how short do you want that distance (length) to be? As short as possible? Alright, I'll give you an approximation by taking the limit as delta-X approaches zero... but i cannot ever reach zero, or the line disappears. Ever notice that "approximate" and "approach" have the same etymological root? Is the word "approach" used in defining anything in mathematics that might apply to derivatives, e.g. "limits"?

I don't think any of this is controversial. Limits are approximations. The limit of (1/x) as x->0 is infinity: does that mean that 1/0 = infinity? The limit of (1/x) as x->infinity is zero: does that mean 1/infinity = 0? That limit notation, describing the value as an approximation, is essential to the validity of the equation.

 

[bpeezer]

(chiral proceeds to steel images from the web)

The definition of a derivative:

The notation "Lim" over "h -> 0" indicates that the output value is derived via approximation. Why the need to approximate? Because at h=0, you have division by zero. Approximating to avoid division by zero is part of the definition. That isn't controversial, is it?

EDIT to add:

Again, the equation to derive the tangent of a curve:

What is delta-X? It is some (measurable, value-associated, direct) distance between 2 points. A line is defined by two points. If delta-x is zero, then there is not two points, there is only one point which is not enough to define a line and the equation ends up with division by zero. Delta-X cannot be zero, it can only approximate it.

Further Edit: an approximation is a description, and "tangent" describes (via approximation) the changing slope of a curve, but it does so conceptually as applied to a single dimensionless point which is not relevant, and the line it generates eliminates the ability to describe the corresponding curve as "convex".
We wish to describe the "terminal angle" of a "convex" bevel. What is a bevel? A sloping surface, a line, a measurable, value associated distance between two points, i.e. delta-X. Well, how short do you want that distance (length) to be? As short as possible? Alright, I'll give you an approximation by taking the limit as delta-X approaches zero... but i cannot ever reach zero, or the line disappears. Ever notice that "approximate" and "approach" have the same etymological root? Is the word "approach" used in defining anything in mathematics that might apply to derivatives, e.g. "limits"?

I don't think any of this is controversial. Limits are approximations. The limit of (1/x) as x->0 is infinity: does that mean that 1/0 = infinity? The limit of (1/x) as x->infinity is zero: does that mean 1/infinity = 0? That limit notation, describing the value as an approximation, is essential to the validity of the equation.

The problem with using the definition of derivative in this manner is that you are evaluating an equation by its denominator, without taking the numerator into account. Rather than trying to describe this to you, I'm including a picture walking through this process. Here you can see inputting an actual function into the definition of a derivative to solve for the particular function's derivative.

You'll notice that I never had to measure h, and there is a clearly defined function describing the tangent slope. No guesswork, no approximation

 

[chiral.grolim]

The problem with using the definition of derivative in this manner is that you are evaluating an equation by its denominator, without taking the numerator into account.
...
You'll notice that I never had to measure h, and there is a clearly defined function describing the tangent slope. No guesswork, no approximation

What does the solution to the equation say? In the answer, it still states "as h -> 0 ..." What does that mean? What does the notation 'lim' over 'h->0' mean? To understand the definition, you must understand the meaning of its constituent parts. The limit notation quite literally describes a process of approximation - a value is being approached, but not reached - and WITHOUT the limit notation, the solution is impossible as it requires division by 0. The solution describes the slope of a tangent by approximating a value - that is what "as h -> 0" means. It is telling you, "This is what the slope of the tangent line would be if a single-point could define a line... which it cannot." *shrug* The tangent is conceptual.

As for the "guesswork", that comes in when you are generating an equation to fit the curvature in order to generate a "clearly defined function" to give you the slope of the tangent. In your example, you assumed a known f(x), namely x^2. Try again without f(x)=x^2. If you don't have that initial equation, you BEGIN with guesswork in creating a best-fit equation for the curve (not a simple task, but required if you expect to make formal adjustments to your derivative by substituting the equation of the line into the numerator) before proceeding to approximate a value based upon it (the derivative itself). It is impossible to solve the derivative without the curve's equation... and the result is STILL only an approximation that is neither relevant (since it applies to a single point not a bevel) nor applicable (since the curve is not "convex" relative to the tangent). Wrong method.

 

[bpeezer]

What does the solution to the equation say? In the answer, it still states "as h -> 0 ..." What does that mean? What does the notation 'lim' over 'h->0' mean? To understand the definition, you must understand the meaning of its constituent parts. The limit notation quite literally describes a process of approximation - a value is being approached, but not reached - and WITHOUT the limit notation, the solution is impossible as it requires division by 0. The solution describes the slope of a tangent by approximating a value - that is what "as h -> 0" means. It is telling you, "This is what the slope of the tangent line would be if a single-point could define a line... which it cannot." *shrug* The tangent is conceptual.

As for the "guesswork", that comes in when you are generating an equation to fit the curvature in order to generate a "clearly defined function" to give you the slope of the tangent. In your example, you assumed a known f(x), namely x^2. Try again without f(x)=x^2. If you don't have that initial equation, you BEGIN with guesswork in creating a best-fit equation for the curve (not a simple task, but required if you expect to make formal adjustments to your derivative by substituting the equation of the line into the numerator) before proceeding to approximate a value based upon it (the derivative itself). It is impossible to solve the derivative without the curve's equation... and the result is STILL only an approximation that is neither relevant (since it applies to a single point not a bevel) nor applicable (since the curve is not "convex" relative to the tangent). Wrong method.

I do not understand how you continually argue against fundamental calculus. This is clearly a waste of my time.

 

[Airborne 1]

While you genesis debate this both my Barkies can shave the fuzz of a nat's ass and that is using a #1000grit and a #6000 grit whet stone...How about yours??


2Panther

 

[Lagrangian]

Not everyone will agree, but that's okay with me. (I know chiral.gromlin still has different ideas about what derivatives and limits are.)

Even so, I wanted to do some more illustration of the ideal convex edge. Although I have not shown it, all the informal points made in the diagram can be proven mathematically. I think it should be fairly obvious to anyone who has taken undergraduate or AP calculus.

Conventional mathematics makes the following points:

(1) If the two sides of the convex edge are differentiable curves, then the angle of the apex is well defined. The angle of the apex is the angle between the tangent on the left-side of the apex and the tangent on the right-side of the apex.

(2) The angle of the apex tells us about the geometry of the apex. The two tangent lines form the most acute angle that shares the same apex and also contains the entire "convex" edge. In this sense, it is the "tightest fitting" angle of the convex apex.

(3) If we were to magnify the apex, the convex edge would become closer and closer to the tangent lines. Under the limit of infinite magnification, the convex edge will converge to the angle formed by the two tangents.

(4) The convex edge is always more narrow than the angle formed by the two tangent lines.
(Sketch of proof: Proof by contradiction (see pictures below): Suppose the convex edge were wider. Then there must be at least one point on the convex edge which is wider than the tangents (but is not the apex itself). Let that wider point be called P. The tangents are the limit of a series of secant lines. At some point in the limit, the secant line will move past point P. Once the secant is past P, the convex edge will be narrower at P. As the limit continues, the secants will get even wider until they converge on the tangent lines. Therefore, the tangent lines are wider than the convex edge at point P. Contradiction. Therefore, no such point P exists. Therefore, every point on the convex edge (except the apex) is more narrow than the tangent lines.)

I hope this is helpful.

Sincerely,
--Lagrangian

 

[BluntCut MetalWorks]

Anthony/Lag; Martin/HH; Chiral; bpeezer; et all :thumbup: :thumbup:

:thumbdn: My foggy math brain :thumbdn: Not looking forward http://en.wikipedia.org/wiki/Uniform_convergence escalation ... hahahaha

 

[Fred.Rowe]

Calculus makes my head hurt, Fred

 

[chiral.grolim]

Points where you fail:

...The angle of the apex is the angle between the tangent on the left-side of the apex and the tangent on the right-side of the apex...

Where is this "angle" applicable to the curve? At a single point without dimension, without area. What is an "angle"? The area between lines. How can a single point form an area between lines? It cannot. To declare that it can is division by zero. Again, this is why the "limit" notation is essential. It is "well defined" as an approximation - a value that is "approached" - and mathematicians are alright with that.

...The angle of the apex tells us about the geometry of the apex. The two tangent lines form the most acute angle that shares the same apex and also contains the entire "convex" edge. In this sense, it is the "tightest fitting" angle of the convex apex.

What is a "convex apex"? This description is meaningless. "Convex" demands a line above which it curves, an "apex" is a point and cannot be "convex" relative to anything. The curved bevels form an apex, as do the straight tangent lines. The tangent lines present an angle, but the curves do not (cannot), the area between them must be derived and the process is one of approximation (as I have clearly demonstrated above) using secant lines to which the curve remains ever "convex", i.e. those lines are ALWAYS thinner. The ONLY place where those lines are NOT thinner is when they cease to be lines at all, converging to a single point which, as I already made clear, is not allowed, and that is well declared in the "limit" notation as I AGAIN previously explained. Once a line is a point, it is not a line.

These are axioms, people, it shouldn't be this hard to grasp, just as the definition of "convex" is not controversial.

EDIT to add: How many sides around a circle, and what is the angle at each vertex between sides? A circle is a polygon with infinite sides of infinitesimal length. What does that mean? It means that each side approaches not being a "side" at all since a side must have length - the length of each is approximately zero. The angle between sides approaches 180-degrees as the number of sides of a polygon increase to infinity, the angle between any two sides of a circle is approximately 180 degrees, i.e. a flat line yet it forms a circle.
How do we find the circumference of a circle? Well, you could measure its approximate circumference using a flexible ruler that converts curved lengths into approximate straight lengths... or you could calculate the value from taking a straight measurement of the circle's radius (no approximation needed) and then multiplying 2(Pi)(r). But wait!! What is this value (Pi) required to give the circumference? Pi is a ratio: circumference divided by twice the radius, area divided by square of the radius. If it is so simple a relation, why don't we know the precise value of Pi? Specifically because of the nature of curves. We measure with straight lines, not curves. The smaller those lines, the more accurate our value for Pi. *shrug*

...If we were to magnify the apex, the convex edge would become closer and closer to the tangent lines. Under the limit of infinite magnification, the convex edge will converge to the angle formed by the two tangents.

No. Emphatically NO.

First, tangent is arrived at via secant lines inside the curve - that is what the process is, understand that. You do not begin with the tangent and then differentiate your way to the equation of the curve, but if you did it would follow the same path - inside the curve.

Second, the curves converge on that intersection POINT. A point is not an angle and cannot form an angle - that requires bevels with length, and there is only an utterly length-less POINT of overlap. In the process of "infinite magnification" the tangent lines and the curves all terminate in a single point without ever having overlapped at a single point elsewhere - the curve approaches flat but never reaches it.

Do you not understand why? Do you not see why the notion of "limits" is essential to the whole concept? You cannot simply skip over the "limit" aspect of a derivative and go from approximation (which is part of the definition) to an absolute, doing so would result in division by zero. That is precisely WHY the approximation aspect is there, it is a convenient way of getting around an impossibility. We define the angle of intersecting curves in the language of approximation - derivatives. It is the only way to do it.

...The convex edge is always more narrow than the angle formed by the two tangent lines.

This is the only part where I agree, and is also part of the reason it is obvious that "tangent" is is the wrong method for comparing a convex grind to a flat grind. Again, have i not made sufficiently clear the definition of "convex"??? Just like ignoring the mathematical language of limits in derivatives, you are ignoring the language used to describe the bevel you've created. Doing so, is absurd and is the same as dividing by zero to give your answer. It should be rejected by anyone with a knowledge of the basic definitions involved in either.

Proof by contradiction (see pictures below): Suppose the convex edge were wider. Then there must be at least one point on the convex edge which is wider than the tangents (but is not the apex itself).

That is a contradiction already, a tangent to a curve intersects at only a single point by definition.

The tangents are the limit of a series of secant lines.

Yes, a limit that is never reached.

At some point in the limit, the secant line will move past point P. Once the secant is past P, the convex edge will be narrower at P.

Again, you are comparing things that do not relate and using contradictions in your description.

1) The secant is the straight-line connecting each point on the curve to the apex. In doing so, said length always falls within the curve, providing that curve the description "convex". The edge is ONLY "convex" relative to that segment of line. Seriously, guys, why do you keep ignoring the definition of the word??? No one has explained that to me yet.

2) The convex edge is narrower, because the secant lines go on for infinity - you are declaring convex edges to be thinner than infinity???? Give me a break. :thumbdn: Where are you drawing your arbitrary line for the length of the secant you are comparing to the convex? This length can NOT be arbitrarily selected, it is defined as the length beneath the curve.


Nothing i am presenting differs from "conventional teaching". Once again, the diagram:

In this diagram, 'T' and 'W' intersect at your point 'P'. Nearer to the apex than 'P' is another point 'Q' which forms an angle through another secant line 'W', and nearer still is another and another until the length of 'W' cannot be measured. At each point on the curve, it is that length 'W' which helps forms the angle. The limit occurs where the apex IS the point between which the length 'W' would extend ... but since there is only a single point, there cannot be a length, and without a length there cannot be an angle, hence the term "limit".


Lagrangian,
Please go through this post, as I did with yours, and point out where I am mistaken, where my understanding differs from convention. Convex cannot ever be thinner than the flat from which it gets the title "convex". Your declaration to the contrary is in and of itself a contradiction, proof sufficient without my having to explain anything math-related, nevertheless I have done so.