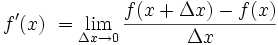Ideal and Real Geometry of Convex Edges

[chiral.grolim]

I do not understand how you continually argue against fundamental calculus. This is clearly a waste of my time.

Were you able to reduce the derivative function without knowing a function from which to derive it?

Did I misrepresent the nature of "limits" or the process of finding a derivative? Did I misrepresent the definition of "convex" or "line" or "point" or "angle" and their application?

You misrepresent my argument in claiming it to be "against fundamental calculus".

 

[bpeezer]

Were you able to reduce the derivative function without knowing a function from which to derive it?

No, that is exactly the point I was trying to make. YOU were reducing the derivative equation without knowing the function, by claiming that:

at h=0, you have division by zero.

I was showing a direct example where applying the derivative equation properly and reducing it algebraically allows for h to equal zero without producing a division by zero.

Did I misrepresent the nature of "limits" or the process of finding a derivative?

Yes

 

[chiral.grolim]

No, that is exactly the point I was trying to make. YOU were reducing the derivative equation without knowing the function, by claiming that:

Trying to understand this point

The equation of the curve is not known. The equation for its tangent is supplied by the very definition of tangent.

The equation declares without any reduction that delta-X cannot equal zero; if it did, there is division by zero. I didn't "reduce" anything, I cited the definition which is applicable to EVERY function, hence "definition". It is not a "claim" I am making.

I was showing a direct example where applying the derivative equation properly and reducing it algebraically allows for h to equal zero without producing a division by zero.

You are wrong.
You showed via a known equation that a derivative could be generated. You also admit that you cannot do this without an equation to work from? And what did the derivative tell you?

In the answer, it still states "as h -> 0 ..." What does that mean? What does the notation 'lim' over 'h->0' mean? ... The limit notation quite literally describes a process of approximation - a value is being approached, but not reached ... The solution describes the slope of a tangent by approximating a value - that is what "as h -> 0" means. It is telling you, "This is what the slope of the tangent line would be if a single-point could define a line... which it cannot.

Maybe this will help: http://mathforum.org/library/drmath/view/70599.html

The only reason that you are able to reduce the derivative algebraically is specifically because h does NOT equal zero. Do you not see this? It is part of the definition.

You disagree with this, the very concept of "limits"? You think that a derivative is NOT an "approach" to a value? THAT is arguing against "fundamental calculus".

Show me how I misrepresented "limits" and derivatives.

Edit to add: Do you accept the definition of "convex", or that a line requires 2 points, or that an angle is a measure of the area between lines? Just what definitions do you accept vs reject?

 

[bpeezer]

Maybe this will help: http://mathforum.org/library/drmath/view/70599.html

Glad you posted this, it proves my point

The quantity whose limit we are taking is undefined at h = 0, for just the reason you say. But the LIMIT at h = 0 exists.

 

[Fred.Rowe]

I never studied Calculus, my background is trig and algebra and that as a field surveyor, so my understanding of the discussion about the correct calculus is vague at best.
I do believe what I stated in the other thread with the OP is the true measure of the argument.

If one holds the the point on tangent and the point on curve and the convex [curve] is laid out using degrees of deflection and cords, with enough stations on the curve, {convex] to make the comparison relate to the size of the study, I don't think there can be any argument. Just add the number of angles along the curve, including the angles that make up the edge profile, subtract two angles and multiply times 180, compare these two sums, the result gives you how the two edges compare, the flat [straight] edge and the curve [convex edge. Is this reasoning not correct? I think the calculus is just grounds for argument where as my rational gives a "true" understanding of how the two edges relate.

Fred

 

[chiral.grolim]

Glad you posted this, it proves my point

Um, no it does not. Your claim was as follows:

I was showing a direct example where applying the derivative equation properly and reducing it algebraically allows for h to equal zero without producing a division by zero.

Now read what you quoted again:

The quantity whose limit we are taking is undefined at h = 0, for just the reason you say. But the LIMIT at h = 0 exists.

Apparently you do not understand the concept of a "limit". "Limit" is an approximation, it is a value that is not reached because the input value for 'h' is not reached. In the definition of a derivative, the notation specifically declares that h never equals zero, it only "approaches" zero. It is only for this reason, that you can reduce the derivative by dividing by "h". THAT is what the sentence "the LIMIT at h=0 exists" means, that we can approximate a value as h approaches zero, specifically NOT that we can calculate a value at h=0. There IS NO VALUE for h=0, there is a LIMIT only.

Why must it be so? Because at h=0, there is no definable line because a line requires 2 points whereas at h=0 there is only 1. An angle requires 2 lines with space between, but at a single point there is neither lines nor space between them. But at the "limit" we simply approximate a very small length (h, or delta-x) from which we get a line, and from two such lines that intersect we can get an angle.

Understand the terms you use, understand their meaning, understand why they have that meaning, otherwise you do not understand the math in the first place.

 

[HeavyHanded]

After chiming in a handful of times, I keep wondering why it is described as necessary that the arc of the convex be referenced to the line of the V bevel. Right off the bat this must make the convex larger at the edge than the V bevel.

I believe it makes more sense to reference it to the centerline, the intersection of this is what creates our final angle and the only real constraint on the entire figure, V bevel or convex. Whether the arc is convex to the V bevel path is not relevant.


When this is done, the tangent of the arc becomes the plane of the V bevel as it intersects the centerline, and the entire remaining path of the convex that matters to the conversation, falls between the tangent and the centerline.

In my diagram, XY is the centerline, AB the tangent (and line of the V bevel), points T and Z are where XY intersects the arc twice and only twice (satisfying the convex definition, and without resorting to segments of a parabola). At no point does the arc exceed 180°. The arc is convex to the centerline.

Both the arc and the line of the V bevel cross XY at 20° (but could be any angle). The tangent is taken from the circumference of the circle at 90° - the point at which the arc is neither nearing nor moving away from AB.

I included a primary and spine for visual clarity, but they don't really need to be there, only the relationship to the centerline XY is critical.

This diagram is a bit different from the curvilinear one I made earlier that shows only the primary/cutting bevel being replaced with an arc and continuing on a straight line to the edge, but both are equally valid. I haven't included any equations, but I don't believe any are needed in this example...

 

[bpeezer]

"Limit" is an approximation, it is a value that is not reached because the input value for 'h' is not reached.

You're right, the limit is a value: a specific, well defined value. This value in our case is the derivative. To take a derivative, we do not care if the value can be reached or not. We care what that value is.

 

[chiral.grolim]

You're right, the limit is a value: a specific, well defined value. This value in our case is the derivative. To take a derivative, we do not care if the value can be reached or not. We care what that value is.

And the "value" of a "derivative" is what? An approximation, a "specific, well defined" approximation. It is the approximation that has a value, and it can only be an "approximation" because it cannot be reached. That is what the use of derivatives tells you - "as h approaches value x, the output approaches this value y". This is the definition of the term "limit". Do you understand why the value cannot be reached?


Since the value cannot be reached, since the value is only applicable to a single point and of no relevance anywhere behind that point, in what conceivable way would it be applicable to the current discussion of characterizing the geometry of a convex edge? The limit (tangent) approximates the angle of intersection of the two curves and is only applicable at a single dimensionless point and nowhere else, nowhere along the bevel is it in any way applicable. It is irrelevant to the discussion except with regard to how it is achieved, which i presented over and over again - through flat secant lines beneath the curve. It is those lines that allow the curve to be called "convex".

 

[ToddS]

Chiral Grolim's explanation is consistent with my recollection of calculus... I admit that I didn't attend a top 10 US University; however, I did have Keith Geddes as a calculus professor.

This is a cross-section of a convex blade:

I want to measure the "apex angle" - how will I do this?
The only way I can see is to measure the angle between secant lines:

I don't see these angle values as useful. I think it is useful to measure the thickness of the blade at certain distances from the apex - thickness behind the edge. That, plus the edge width or radius, defines the blade geometry.

 

[chiral.grolim]

...I keep wondering why it is described as necessary that the arc of the convex be referenced to the line of the V bevel. Right off the bat this must make the convex larger at the edge than the V bevel.

YES!!! :thumbup::thumbup: As to why it is "necessary", the word "convex" is defined that way. It is axiomatic, it is part of the definition. To use it any other way is inappropriate and results in immediate contradiction.

Whether the arc is convex to the V bevel path is not relevant.

No, the arc gets its "convexity" FROM the "V bevel path", that is the ONLY line of relevance. What is a "concave edge"? Try drawing that with reference to only the centerline. The centerline is decidedly NOT relevant.

In my diagram, XY is the centerline, AB the tangent (and line of the V bevel), points T and Z are where XY intersects the arc twice and only twice (satisfying the convex definition, and without resorting to segments of a parabola). At no point does the arc exceed 180°. The arc is convex to the centerline.

The arc is only "convex" to the center line between points T and Z. Beyond points T and Z, it is no longer "convex". AT NO POINT is the arc convex to the tangent line AB. AB is not relevant to the arc's "convexity".

 

[chiral.grolim]

I don't see these angle values as useful. I think it is useful to measure the thickness of the blade at certain distances from the apex - thickness behind the edge. That, plus the edge width or radius, defines the blade geometry.

:thumbup: Evidently Gillette didn't see them as useful either. Keep up the awesome work, ToddS. Your website may become a definitive source of material for educating people about the geometry of knife edges, thank you for starting it.

 

[bpeezer]

Since the value cannot be reached, since the value is only applicable to a single point and of no relevance anywhere behind that point, in what conceivable way would it be applicable to the current discussion of characterizing the geometry of a convex edge?

When taking the derivative of a differentiable continuous function, it will describe the tangent slope of any point along that function. In an ideal apex scenario with infinitely accurate measuring equipment, you can characterize the function that defines the bevel and determine the apex angle. I never once claimed that the apex bevel actually matters, just that it can be determined under ideal conditions.

 

[HeavyHanded]

The arc is only "convex" to the center line between points T and Z. Beyond points T and Z, it is no longer "convex". AT NO POINT is the arc convex to the tangent line AB. AB is not relevant to the arc's "convexity".

Excellent, we agree on something!

Are you implying that a convex shape must be convex to any given line indefinitely? This is not possible - lines intersect convex forms without making them "unconvex" as long as they only cross in two points...

AB is not relevant to the "convexity" of our arc except as its tangent. Is easy to see if we make a line convex to AB, it will start out more broad at the apex than a straight line, yet it is has no bearing on reality - just look at the diagram.

And yes, the only line that does matter for reference is the centerline - how else do we derive our cutting angle, how do we determine what the primary angle is?? As I stated, referencing the convex it to its own tangent makes as much sense as referencing it to any other arbitrary line drawn off the centerline - meaningless.

It is convex to the centerline in the same way a hollow grind is concave to the centerline - what else would you use for reference - the spine, the cutting edge? A hollow grind is not concave to the cutting angle in the same way a convex is not convex to the cutting angle.

All must be referenced to the centerine, Just look at the backside of the arc and there you have the concave equivalent. I'd highly recommend adding a little meat to it at the cutting edge with an additional bevel though...

 

[chiral.grolim]

When taking the derivative of a differentiable continuous function, it will describe the tangent slope of any point along that function. In an ideal apex scenario with infinitely accurate measuring equipment, you can characterize the function that defines the bevel and determine the apex angle. I never once claimed that the apex bevel actually matters, just that it can be determined under ideal conditions.

Explain to me this notion of "infinitely accurate measuring equipment". The tangent is relevant at a single point - it has NO dimensions, there is NOTHING to measure, not even under "ideal conditions". It does not have infinitely small dimensions that could be measured by ANY equipment under ANY conditions, ideal or otherwise, because the very "idea" of a point is that it is dimensionless. Your "infinitely accurate measuring equipment" would be measuring infinitely small lengths connecting two points on the curve = secant lines.

 

[Lagrangian]

Hi everyone,

To keep the discussion clear, we should separate the discussion into two topics:
(A) Ideal Mathematics
(B) The Real World

---------------------------------------------------------------------------------------
A few points about ideal mathematics:
(1) In conventional math we say

If f(x) = x^2
Then f'(x) = 2x.

This is not an approximation. There is no modern textbook (graduate or undergraduate), nor any mathematician who says f'(x)=2x is an approximation. It is exact. (If you disagree, it is probably best to debate this in math class, rather than in a knife forum?)

(2) The invention of the derivative is non-trivial; mathematicians spent years figuring out a mathematically rigorous way to define and study limits. There were a lot of debates. Just a few giants in the field would be Newton, Leibniz, Cauchy, Riemann, Weierstrass, Cantor, etc.

(3) The reason calculus was an amazing invention, is that it gave a mathematically precise definition of derivatives. It became possible to mathematically describe "instantaneous velocity" of an accelerating object. Once the notions of derivative, integration, and limits became rigorous, the whole field exploded.

(4) Mathematicians have no problem saying,"Suppose f(x) is some arbitrary differential equation..." and then proving theorems about the derivative f'(x). For example, one version of the Fundamental Theorem of Calculus is:
integral(f'(x)) = f(x) + c for some constant c.

The Fundamental Theorem of Calculus is not an approximation. It is exact. I don't think you will be able to find any textbook or mathematician who says otherwise.

Notice we did not have to know much about f(x) other than it is differentiable. So mathematicians can talk rigorously about the derivatives of functions even in the abstract, where f(x) is not fully specified.

Because the above points are taught (and proven) in every calculus textbook I've seen, every mathematics class I've taken (including homework sets, exams, and projects), every mathematically technical website I've seen, and is the same understanding as every student, professor, engineer, and scientist I've come across, I say this is part of "conventional" mathematics. The only disagreement I've seen is from Prof. Wildberger on YouTube. His views are reasonable, but unconventional, and I'm OK with them. Here's a youtube of his about this.
https://www.youtube.com/watch?v=fCZ8jJCVinU

---------------------------------------------------------------------------------------
A few points about the real world:

(1) It is perfectly valid to debate whether ideal mathematics is relevant to the real world. In my opinion, mathematics is our most powerful tool for describing and quantifying what happens in the real world. If our mathematical models do not match the real world, then we should improve them with better models (usually involving additional math that accounts for additional effects).

(2) If we really want to talk about the real world, then ToddS and Verhoeven's micrographs are a good place to start. Ultimately, the structure of the knife is atomic, and I don't think we have any disagreement in general, about the real-world.

(3) In ideal math, both a V-edge and a convex edge have well defined angles at their apex. In the real-world, they do not. (Just look at the electron micrographs.) This is why I like to keep the two discussions separate.

In many forum discussions, people talk about the angle of the v-edge as if it were a mathematically ideal edge. We know in the real world, that this is incorrect. The whole point of my original post is that exactly the same thing happens for convex edges: It is possible to talk about the apex angle of a convex edge as if it were ideal math. But in the real world, we know this is wrong.

---------------------------------------------------------------------------------------

I'm reluctant to go down the rabbit-hole of trying to teach calculus in a knife forum. Probably a classroom is better for that.

That said, if you find the notion of derivative to be unintuitive or seemingly "paradoxical," then you are in good company. It took some of the most brilliant mathematicians years and years to figure out how to make it mathematically rigorous and precise.

Almost every student (including myself) was at least a little puzzled the very first time they the formal definition of a limit (which uses epsilon-delta): (from wikipedia: http://en.wikipedia.org/wiki/Limit_of_a_function)

If this definition is new to you, and completely intuitive, then congrats! You're probably in the 99+% percentile of math students.

For a knife forum, I do not see any point in doing formal math here. Instead, I try to make diagrams and pictures, which I hope are intuitive and easy to understand.

chiral.gromlin and I disagree about what a limit is, and because a derivative is a limit, we also disagree about what derivatives are. I think that's okay. I mean, at least it is okay with me.

Sincerely,
--Lagrangian

 

[Lagrangian]

I never studied Calculus, my background is trig and algebra and that as a field surveyor, so my understanding of the discussion about the correct calculus is vague at best.
I do believe what I stated in the other thread with the OP is the true measure of the argument.

If one holds the the point on tangent and the point on curve and the convex [curve] is laid out using degrees of deflection and cords, with enough stations on the curve, {convex] to make the comparison relate to the size of the study, I don't think there can be any argument. Just add the number of angles along the curve, including the angles that make up the edge profile, subtract two angles and multiply times 180, compare these two sums, the result gives you how the two edges compare, the flat [straight] edge and the curve [convex edge. Is this reasoning not correct? I think the calculus is just grounds for argument where as my rational gives a "true" understanding of how the two edges relate.

Fred

Hi Fred,

I'm not 100% sure I understand what you mean, but I think I do. Intuitively, I think you are saying: Imagine we walk along some (smooth) curve. We can simply keep track of how much we turn left or right in degrees. If we can't do this, well, we can put some stations on the path and measure the angle between adjacent line-segments between nearby stations. By adding up all the angles between adjacent line-segments, we can find the angle of the last line-segment.

That's correct. Then in calculus, we simply use an infinite number of stations. That is, we start adding more and more stations, and take the limit as the number of stations goes to infinity. During this process, we will see that the angle of the last line segment converges to a limit, which is the derivative.

It's a slightly round-about way to think about it, but it works.

Sincerely,
--Lagrangian

 

[Fred.Rowe]

Hi Fred,

I'm not 100% sure I understand what you mean, but I think I do. Intuitively, I think you are saying: Imagine we walk along some (smooth) curve. We can simply keep track of how much we turn left or right in degrees. If we can't do this, well, we can put some stations on the path and measure the angle between adjacent line-segments between nearby stations. By adding up all the angles between adjacent line-segments, we can find the angle of the last line-segment.

That's correct. Then in calculus, we simply use an infinite number of stations. That is, we start adding more and more stations, and take the limit as the number of stations goes to infinity. During this process, we will see that the angle of the last line segment converges to a limit, which is the derivative.

It's a slightly round-about way to think about it, but it works.

Sincerely,
--Lagrangian

Thanks for the response. Wanting to make this as clear as I can; I say there is an exact correlation between the sum of the angles in side a convex edge, compared to the sum of the angles contained inside a flat edge with both having the same dimensions, height of edge/distance across shoulders. I've closed hundreds of field surveys and believe comparing two edges in this manner will result in a number which shows how sharp one edge is compared to the other. Simple math. I like math for this reason, its exact.

With a convex edge, it does not turn left or right, It's like NASCAR, its always the same direction

 

[bpeezer]

Explain to me this notion of "infinitely accurate measuring equipment". The tangent is relevant at a single point - it has NO dimensions, there is NOTHING to measure, not even under "ideal conditions". It does not have infinitely small dimensions that could be measured by ANY equipment under ANY conditions, ideal or otherwise, because the very "idea" of a point is that it is dimensionless. Your "infinitely accurate measuring equipment" would be measuring infinitely small lengths connecting two points on the curve = secant lines.

You don't measure the tangent, you calculate it.

 

[chiral.grolim]

A few points about ideal mathematics:
(1) In conventional math we say

If f(x) = x^2
Then f'(x) = 2x.

This is not an approximation... It is exact.

Here is what I would like you to do:

1) As I asked before, reply to one of my posts point-by-point to find the error. I've replied to a number of your posts point-by-point to show you each contradiction in your thinking, why are you not able to do likewise?

2) Explain to me what you understand f'(x) = 2x to mean. Better yet, do you understand that this is an accurate explanation of it? "The limit of f'(x) as delta-X approaches zero is 2x." Tell me, when does f'(x) equal 2x? When does delta-X reach zero?



When you say that a derivative "is exact", what you are saying is, "this is the theoretical value at the limit of our approximations." It should be intuitive that a single point cannot form a line, that is part of the definition of lines and points, and doing so requires division by zero, which is precisely why LIMITS must be used. It should also be intuitive that curves cannot form angles which is why we use LIMITS to approximate an angle of intersection by theorizing straight lines in place of the curves.

Understand that "limits" are a process of approximation, which is why we call it a "limit" and use the word "approach" in the definition.
I am not saying a derivative value, i.e. the slope of the line formed by the equation, is not "exact". What I am saying is that that slope as it applies to the curve is not reached, it is only approached. What is reached? Approximately that value. Why only approximately? Because a "curve" cannot ever form a "line" with a slope or it would cease to be a "curve". The definition of the derivative directly declares it to be an approximation. It can be done no other way, and THAT is in "ideal mathematics".

You seem intent on declaring that values approached are reached, which is a direct contradiction of the math and results in division by zero. "Tangent" is the concept of a line touching a curve at a single point. A single point is insufficient to define a line, so the "exact" slope of such a line is theoretical and can only be defined through the process of approximation known as "limits".

And again, since the slope of a tangent is only applicable to the curve at that single point to which it corresponds, it is irrelevant to every other point on the curve, irrelevant to any measurable length of the curve, and so is irrelevant to the geometry of the curve and SHOULD NOT BE USED to describe the cutting angle or "terminal angle" of a convex edge.