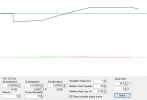
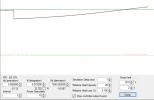
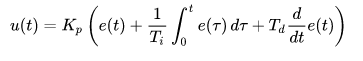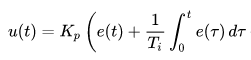Finally, time to talk about the
integral portion of PID controllers.
I do not like this mathematical form, but because most (if not all) of the commercial PID controllers use use it, I need to introduce what is known as the “standard form” of the PID algorithm:
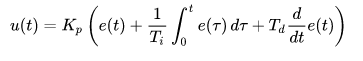
Because I am not for now going to talk about the derivative function, I will cut that out, and shorten this equation to the following:
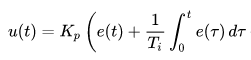
Here, as before, u(t) is the instantaneous value of the output of the controller, which can be of any value, positive, or negative, but if greater than 100, just becomes “100” (because you can not turn that heater on any more than max), and if negative, becomes “0” (unless you have refrigeration handy). Kp is the same as before (the proportional constant), but now we have a new thing, “Ti” which is called the “integral time” (more about this later). Notice that because of the parenthesis, the Kp actually multiplies the integral term, so that the term in front of the integral actually is “Kp / Ti”
Going back to a “word-form” of the equation, this reads like this:
Controller output = Kp * (current difference in temperature from the setpoint)
+ (Kp/Ti) * ( the sum of ALL previous differences in temperature from the setpoint)
(again as with the other form, deviations from setpoint to lower temperatures are taken to be
positive values. This starts getting really important with the integral term)
So – what is the “sum of all previous differences in temperature from the setpoint” ??
The wording is a little misleading.
This really means multiplying the difference from the setpoint by the amount of time that difference was present.
It is kind of like driving a car. You have somewhere to go, and the speed limit is 60mph (yes, in this example you are driving at 60 max ). You find yourself day dreaming about that next knife you are going to design, and your speed drops to 55 mpg (5 mph below “setpoint”). And you do not notice for 5 minutes. You are behind (distance wise) from where you “should” have been. But … you are not “5 mph” behind (you can not “catch up” to where you “should be” by just going back up to 60 mph). Neither are you “5 minutes” behind (you can not “catch up” by just driving 5 more minutes, because the amount of distance traveled at 55 is less than you “would” have traveled at 60 mph).
What you are is (sorry about this) 5 mph * 5 min = 25 mph-min (the product of the two) behind where you should be. You know this intuitively when you step on the gas and go 70 until you are “caught up” … but the PID algorithm does this math explicitly.
The algorithm is not really even doing an integral – it is just keeping an ongoing sum, based on the multiple of the Cycle Rate (remember that from the last post) and the “current error from setpoint” at the end of the control cycle.
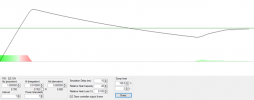
Lets take an example of an oven running at a setpoint of 100 degrees (F) and with a cycle time of 2 seconds. All is fine, then at “time 0” something happens (element burns out, the wind cooling it picks up a lot, you spill your full cup of iced tea on it (that was for you southerners)) and the thing starts cooling. Two seconds later, when the cycle time has expired, a plot of what happened looks like this:

The controller is going to say “the temperature has been too low by 10 degrees for 2 seconds, so the accumulated error is 10 degree * 2 sec =
20 degree-sec. things (for some reason) continue cooling off, and in another 2 seconds the temperature is now down to 80 degrees:

The controller is going to now “say”: “I have been below setpoint by 20 degrees for two seconds (the two seconds since the last beginning of a control cycle), or 20 degrees * 2 sec =
40 degree-sec.
It takes this, and ADDS it to the previous recorded total error of 20 degree-sec, or:
20 degree-sec + 40 degree-sec =
60 degree-sec (accumulated error).
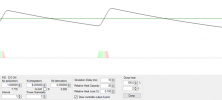
Things continue cooling off for another 2 seconds, bringing the oven now to 70 degrees:

NOW, the PID is going to say: “I have been below setpoint by 30 degrees for 2 seconds”, or 30 degrees * 2 sec =
60 degree-sec.
It takes this and adds it to the previously calculated accumulated error (60 degree-sec), or:
New accumulated error = old accumulated error + new incremental error
120 deg-sec = 60 deg-sec + 60 deg-sec
So the new accumulated error is now 120 degree-seconds.
From here, the PID just goes merrily along, adding new error to the accumulated error sum as long as the temperature is below the setpoint.
So what happens when the temperature finally gets back up to the setpoint?????
Lets continue this (very hypothetical example) and assume that at the next control time (in this case the 8 second mark), the oven temperature has miraculously returned to setpoint
, and the “current error” is now zero.
We need to go back to our “word equation”:
Controller output = Kp * (current difference in temperature from the setpoint)
+ (Kp/Ti) * ( the sum of ALL previous differences in temperature from the setpoint)
In this hypothetical example (with the instantaneous return to the setpoint), the
“current difference” is zero when the setpoint is reached. HOWEVER, the “sum of all previous errors is “120 degree-sec”. Lets assume for now that this weird ratio of Kp/Ti equals 1.0 then in our word equation we have:
Controller output = 0
+ 1.0 * 120 degree-sec
= 120
Even though the temperature is at setpoint, the controller output is 120, which since it is greater than 100, is just effectively 100 – or “full on” for the electric element.
The oven just goes merrily on heating even though it is above setpoint.
While the oven is above setpoint, the contributions to the accumulated error are negative, but it will take some time for the accumulated error to return to zero, and
until that happens, the value of the “controller output” will be greater than zero – and the heating element will continue to be “on” for some (or all ) of the control period (cycle period).
An important point to keep in mind is that this “running sum” of accumulated error starts the second the PID is turned on (or maybe, if you are lucky, when the setpoint is changed – but the manuals do not say…..). So – if you have an oven that is fully cold, and you turn it on, and it takes a long time to come up to setpoint that accumulated error term can be huge … and force the oven to just continue heating for a long time, even if the oven is well above setpoint (this I think is possibly what happened with Ken with his lead melting pot continuing to heat even when above setpoint).
Another thing that can happen is that if the oven is over setpoint for long enough, a big
negative accumulated error can accumulate, which will force the controller output to be negative (i.e. “off”) even when considerably below the temperature setpoint. In this case, you can get into some really weird large up-and-down swings around the setpoint, while that accumulated error term while that accumulated error “lags behind” and forces a delay in when the heating element turns off or on.
Oh … and that weird ratio of Kp/Ti ? Well, it is just the way it is with that form (the term Ti is supposed to have some physical meaning (the time the exponential term will take to return the temperature to setpoint- hence its units are "seconds" - but it does not work that clearly in practice). But, if the manual for your controller says that the units of Ti are "seconds" - then you KNOW the controller is using this "standard form". You have a little bit of a difficult time with this form, because the values of BOTH Kp and Ti affect how much influence the integral sum has… and you can NOT turn off the integral term, because you HAVE to have Kp greater than zero (otherwise you do not have a proportional band defined), AND you can not set Ti equal to zero (because 1/zero = infinity). In the case of the Auber controller, all you can to is set the value of Ti to the largest value (1999 seconds), and hope that you have reduced the integral term to a minimum contribution.
I’m out of time again. The above was mostly words, but hopefully it made sense for the most part. Tomorrow I will try to pull out that PID emulator and give some examples of what this term is doing. I suspect that right now I am saying the term is just “bad”. Not true – under the right circumstances it can help create really, really tight control at the setpoint. But under the wrong circumstances it can create some real havoc that just looks unexplained (until the above helps you to understand what it might be doing in your circumstance…..)