Degree of Sharpness?

[Fred.Rowe]

I'm not a math wiz, by any means, but I was a surveyor for a dozen years. When considering the merits of convex edges compared with flat edges I put forth this thought.
In surveying, when closing a survey to find the total degrees contained inside the survey, you take the number of angles, minus two times 180, equals the number of degrees contained inside the survey.
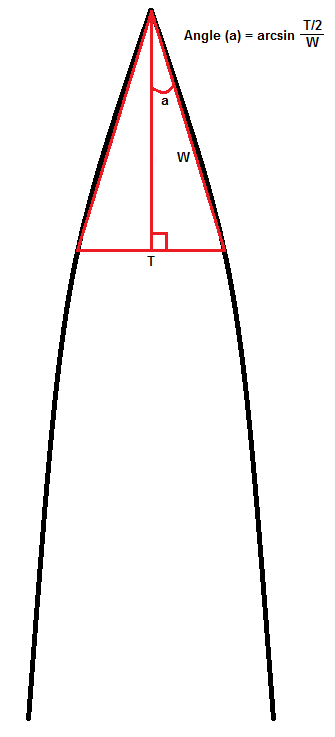
If you apply this to the primary and secondary bevels that make up a knife blade its easy to ascertain the total degrees inside the blades end on profile. In the case of the blade below with its 30 degree inclusive edge, the flat edge itself contains 180 degrees. Number of angles 3 - 2 x 180 = 180
I believe that if you want to compare a convex edge over laid on this 30 degree flat edge it would be more accurate to compare the degree of sharpness between the two edges, first. I think this can be accomplished by adding the degrees contained in the curve of this convex edge and compare the sum to the degrees contained in the flat ground edge. Its a problem of proportion. This is of course is hypothetical, I don't know of a way to measure the actual curve of a convex edge, but I do believe the reasoning is sound.
Once the proportion is found, this number could be used to lengthen the "X" dimension on the flat ground edge which would make the blade thicker at the shoulders, as well as making the flat ground edge angle more obtuse. The angle would increase, it would not be 30 degrees anymore. This would give a more accurate comparison of the two; the convex edge and the flat ground edge. This adjustment along the "X" dimension would result in the two edges being at the same degree of sharp. They should cut the same.

Even though this is a hypothetical problem when I spent some time looking at it in this manner it gave me, what I believe, is a more objective view of this oft compared duo.

What do you think, Fred

 

[bdmicarta]

This will start another war...
I think I understand the geometry but even if someone thinks they understand, it is very hard to explain verbally. I like the convex edge that my old Blackjack has, and one of the sharpest folders I've bought used came with a convex edge. When I reprofile a knife I use a guided system so my bevels are pretty uniform, the opposite of convex.

 

[Fred.Rowe]

This will start another war...
I think I understand the geometry but even if someone thinks they understand, it is very hard to explain verbally. I like the convex edge that my old Blackjack has, and one of the sharpest folders I've bought used came with a convex edge. When I reprofile a knife I use a guided system so my bevels are pretty uniform, the opposite of convex.

I hope thats not the case, my interest is in conversation about interesting concepts. The question is not which one is superior to the other, but instead it's how they compare objectively.

Fred

 

[Jason B.]

The problem is always in the drawing, the convex is too far outside the V bevel. For it to be as thick as shown in the above drawing the blade stock would need to be much thicker than the V beveled blade. If you sharpen a convex edge to the same apex angle then it's always thinner than the V bevel.

 

[bpeezer]

The problem is always in the drawing, the convex is too far outside the V bevel. For it to be as thick as shown in the above drawing the blade stock would need to be much thicker than the V beveled blade. If you sharpen a convex edge to the same apex angle then it's always thinner than the V bevel.

I think Fred is looking from the flipside of the coin. If they both have the same apex angle, the convex edge will be thinner. However, if they both have the same X and Y dimensions (based on Fred's drawing), the convex edge will be thicker.

Fred, are you saying that the comparison should be the apex angle of both geometries? Or are you saying that we should determine sharpness based on the X and Y dimensions? Or maybe something else entirely

 

[Fred.Rowe]

I think Fred is looking from the flipside of the coin. If they both have the same apex angle, the convex edge will be thinner. However, if they both have the same X and Y dimensions (based on Fred's drawing), the convex edge will be thicker.

Fred, are you saying that the comparison should be the apex angle of both geometries? Or are you saying that we should determine sharpness based on the X and Y dimensions? Or maybe something else entirely

I'm looking at how sharp the different edges are when the X - Y dimensions are equal. With this in mind, I believe that if one can measure the curves of the convex edge using degrees of deflection and cords, [the distance between the points on the [convex] curve, add those together and compare that to the degrees contained inside the flat edge; this will give you a fraction or a proportion. The fraction or proportion will be indicative of how sharp one edge is to the other. As an example:
Convex edge degrees 181.35 [measured inside the edge]
Flat edge degrees 180.00 [measured inside the edge] This is just meant as an example and not an actual measurement.
Written out one would say the convex edge is .99255 as sharp as the flat ground edge when using the same geometry.

I'm not interested in proving superiority of either edge, this is a hypothetical way of looking at something that all of us here are interested in. Think of the edge in terms of degrees and distance in stead of the apex itself.
My son Kevin and I have been discussing this for a while and I wanted to share a different view, a dozen years of surveying will do strange things to the way you look at math problems.

Fred

 

[HeavyHanded]

The problem is always in the drawing, the convex is too far outside the V bevel. For it to be as thick as shown in the above drawing the blade stock would need to be much thicker than the V beveled blade. If you sharpen a convex edge to the same apex angle then it's always thinner than the V bevel.

This is all you need to know on the subject IMHO. It becomes a tit for tat until the V bevel becomes a FFG with just the one primary/cutting bevel. Only at that point can one no longer fit a convex inside the cross section area. At the same terminal angle and all other dimensions being equal, the convex will always be thinner.

 

[HeavyHanded]

Add to my above post,
A good trial that might show the benefit/detriment could be seeing at what point, at what combination of primary and cutting bevel angles on the V grind with the same spine thickness and same width, does a convex show no increase in cutting efficiency on a range of common materials.

One could also make some criteria for inducing and testing lateral stress to find out at what stage (if any) the V bevel stand out as being stronger at the same terminal angle.

 

[Fred.Rowe]

The problem is always in the drawing, the convex is too far outside the V bevel. For it to be as thick as shown in the above drawing the blade stock would need to be much thicker than the V beveled blade. If you sharpen a convex edge to the same apex angle then it's always thinner than the V bevel.

This is all you need to know on the subject IMHO. It becomes a tit for tat until the V bevel becomes a FFG with just the one primary/cutting bevel. Only at that point can one no longer fit a convex inside the cross section area. At the same terminal angle and all other dimensions being equal, the convex will always be thinner.

Good morning Gentlemen,

I believe if we are making comparisons between different edge grinds its important to use the same geometry. I agree that if one compares apexes of "roughly" the same angle, [one can't really state a specific edge angle when referring to a convex edge] the convex edge will be thinner.

When the geometry is controlled, the shoulders "X" and height of edge "Y" are constant the flat ground edge will cut better all things being equal. I believe one way to make this point more clear; if instead of a flat ground edge or a convex edge, let's instead put a concave edge on the same blade with the same X-Y geometry. The concave edge will have a better degree of sharpness than either the flat ground edge or the convex edge.

I put many convex edges on blades especially heavy use blades and don't make claim of one being better or worse than the other. This is a discussion that comes out of my love of math and years of surveying. If you would, take a moment to make a simple sketch where you can look at this from the viewpoint presented, where its the sum of the degrees holding the same geometry. the concave has the highest degree of sharpness the flat ground is next and the convex edge will have the least degree of sharp when all the geometry is equal.
Thanks for taking the time to post, Fred

 

[HeavyHanded]

I understand the POV you are expressing, but for this:

the concave has the highest degree of sharpness the flat ground is next and the convex edge will have the least degree of sharp when all the geometry is equal.

to be true, the V bevel would have have a thinner terminal apex. Consider the initial diagram you posted:

The terminal apex angle on the V bevel might be 30*, but the convex overlay is more than twice as broad as the V bevel. You could slice down the centerline and just one half of the convex would be very close to the V bevel 30* (would actually still be a touch larger) but with far less material behind the edge. Taking the half slab of convex down to the same terminal angle would only accentuate the difference.

As a person that does sharpening, think of it this way. An individual comes into your shop with a piece of flat stock with 1/8" spine, 1 1/4" wide. They ask you to put a convex edge on it that is 45* at the apex - this is critical, it cannot go less than 45* at the edge, 22.5" on either side. They don't want an angled primary grind, just convex it into the apex.

They leave and you get to work. You make short work of it. They call back and say they changed their mind after reading this thread, and now want a V bevel but still 45* apex with flat sided primary and keep it at 1 1/4" from cutting edge to spine. Without shrinking the spine to apex dimension, or making a steeper primary grind, it cannot be done - the material that would have made up the shoulders is already gone - doesn't matter what the shape of the arc is that forms the convex, as long as it finished at 45*.

You can convert it back to a V bevel, but only if you angle the primary grind angle into the cutting edge transition (including hollow grinding), make the terminal apex smaller, or grind back up the primary toward the spine until you're clear of where the convex begins.

Using this example, you could use any terminal angle you want in the example - every time they call back and want the V bevel again, you are left with the same set of options until you are down to a perfectly flat grind from spine to apex with the terminal angle predetermined by the spine width. Only at that point would you have to thin the spine in order to place a more acute convex within the target area, otherwise simply grinding off the shoulders will always leave you with less material than behind a V edge of the same terminal angle...

Martin

 

[ToddS]

Having thought about this topic quite a bit while measuring the geometry of convex blades, I would offer the following images:

Convexing blade on a pasted strop produces a geometry approximated by the following image:

Translating the convex (blue) to the same apex as the original (red) shows the expected result, the convex is thicker behind the edge.
An important (mathematically) point here is that there is no "terminal apex angle" in this case. This is why the arguments invoking the terminal apex angle are problematic.

If you partially "convex" the blade by simply knocking down the shoulders and not touching the original apex, you get a geometry (blue) that is thinner behind the edge (some distance from the apex).

However, if you simply flatten that convex part of the bevel, you get an even thinner edge (green). As a surveyor, you will know that a straight line is the shortest distance between two points.

One of the challenges with quantifying sharpness from the geometry is that there are two (somewhat independent) aspects of the apex: the angle (or thickness behind the edge) and the keenness (or edge width). The relative contribution of each to the perceived "sharpness" will depend on the material being cut.

 

[HeavyHanded]

I am not sure why a convex edge would be any more rounded than a V bevel at the apex. One can create one with a diamond plate, a soft backing under flexible media is not required. I am pretty used to crafting convex on a hard surface and can produce a target terminal angle with as much precision as any other edge grind.

Also note the green lines that are more thin behind the edge do not appear to contact along the spec'd terminal angle (in fact cannot based on where they started if one is trying to keep the edge angle the same), but form a bridge making an additional bevel. We are now very close to making a convex edge anyway.

I included an additional line to your art, the orange one would be more typical of a convex arc that stops just short of the apex. To now fit a thinner V bevel into the remaining space one would need to make a full flat grind or something very near to it.

This is part of my point, it becomes tit for tat as the convex and V bevel both morph closer to a FFG with one important (or maybe not) distinction. The FFG V bevel will continue to become more acute at the apex and the convex will do so only as it is completely flattened out.

FWIW, I am no hard-core booster of convex in an absolute sense. In my opinion they excel on thicker stocked tools, and for chopping in general. Once the thickness of the stock is fairly thinned out, it conveys less and less benefit based on my experience, and if taken too far will result in loss of lateral stability at the same terminal edge angle of a V bevel with the same thicknesses above the grind region. I actually believe the V bevel is more durable in some cases and am not entirely clear on why the convex has a reputation for being stronger overall when it can fall in a range of geometries just like a V bevel, some of them being quite delicate.

 

[Fred.Rowe]

I'm still here. We cut our DSL line, digging a drain pipe, so no computer since yesterday.

We are driving to the steel mill to pick up aluminum for the Bubble Jig today; I'll post this evening guys. Good conversation.

Fred

 

[HeavyHanded]

Fred,

I went back and reread your original post on this, based on the measurement criteria you outlined I believe you are entirely correct. The X / Y dimension you are using as the baseline is a constraint on how far back the convex curve can start. Basically with the same shoulder height/bevel width, the V bevel will always be thinner behind the edge than the convex.

All of my considerations on this topic began with the same terminal angle and work up. This leaves potentially far less material behind the edge based on shape of arc and how far back one grinds, but at a minimum will always be less than the V bevel.

Martin

 

[Twindog]

It's true that when the edge height and shoulder width are held constant, a V edge will always be more acute than a convex edge.

But both V edges and convex edges come in a wide variety of geometries. A V edge can be extremely acute or obtuse. It can be a hybrid of angles and bevels.

Likewise, a convex edge can be extremely acute or obtuse. And it can also come in a wide variety of arcs that intersect to form very acute or very obtuse edges.

And convex edges and V edges and concave edges can be so similar to each other that there is no practical way to distinguish their geometry or acuteness or cutting ability. We can also have edges that are a combination of arcs and angles.

The key is not whether an edge is convex or concave or V. None of those edge grinds are inherently better or worse than the other. The key is the actual geometry of the edge and how well that geometry matches the steel, the steel's heat treat and the task at hand.

 

[chiral.grolim]

All of my considerations on this topic began with the same terminal angle and work up...

Just to assist in the confusion, it should be understood that the "terminal angle" is ALWAYS, I repeat ALWAYS 90-degrees per side, i.e. EVERY knife edge has a rounded-over apex with a diameter that in a steel knife is, at best, ~0.1 microns thick.
Back from that apex, "angle" is determined by measuring the thickness of the edge at a given distance back, and a flat bevel will always fit inside a convex bevel because that is precisely what the term "convex" means, likewise a concave bevel will fit within a flat bevel because that is what the terms mean. It is literally impossible for a "convex" edge to be thinner than the properly associated flat edge.

Take as reference the patent info from Gillette for one of their razors: http://www.google.com/patents/WO2013010049A1

... coated blade comprising a cutting edge being defined by a blade tip having a tip radius of from 500 to 1500 angstroms, said coated blade having a thickness of between 0.3 and 0.5 micrometers measured at a distance of 0.25 micrometers from the blade tip, a thickness of between 0.4 and 0.65 micrometers measured at a distance of 0.5 micrometers from the blade tip, a thickness of between 0.61 and 0.71 micrometers measured at a distance of 1 micrometer from the blade tip, a thickness of between 0.96 and 1.16 micrometers measured at a distance of 2 micrometers from the blade tip, and a thickness of between 1.56 and 1.91 micrometers measured at a distance of 4 micrometers from the blade tip.

Note how they never mention "angle" anywhere in there? "Angle" is merely a measurement of area calculated from the thickness at a given distance back from an apex. Here is a picture I posted in another "war" thread:

This is how the "angle" of a convex edge is measured - using straight lines from the apex to some distance back from the apex, with the lines necessarily fitting within the curvature of the grind. The goal in accurately describing the angle of a convex edge is using the shortest distance possible between the apex and where thickness is measured (i.e. shortest 'W' able to be measured practically).

 

[chiral.grolim]

... I actually believe the V bevel is more durable in some cases and am not entirely clear on why the convex has a reputation for being stronger overall when it can fall in a range of geometries just like a V bevel, some of them being quite delicate.

Again, this is only the case when comparing geometries that are dissimilar. "Convex" is necessarily (by definition) thicker than V (flat) and thus has the well-earned reputation for durability/strength associated with having more material support. That is the purpose of the Gillette patent cited above - a convex bevel on a delicate razor to increase durability via increasing thickness/material-support to the apex compared to the fragility of a comparable flat-bevel that has less material support.

 

[HeavyHanded]

I am still not clear on why the convex would be thicker than any flat sided approach until one reaches a straight line.

Anywhere two angles/planes meet, one could define a distance from the angle on each plane and there is a region where a convex arc could be inserted which will remove the joined angle and thus remove surface area or mass. This might be at very small levels, and so I say as one approaches the FFG the differences between the edge grinds matters less and less.

If one defines the final approach angle at some fixed distance (from the 90° region that defines all edges at their terminus) no matter how minute, the straight sided approach will be limited by the angle where the planes meet, the shoulder transition. The convex suffers no such handicap. It also needn't be defined as a fixed radius that arcs to the bitter end - it can be straightened out for the final approach and still be a convex for purposes of the discussion, or viewed as a segment of a parabola.

If one uses X/Y dimensions per the OP, the convex will come in dead last. However, every joining of two planes, at any angle, will leave a region that can be bridged by an arc. Only a single straight line is free of this condition - that's why there's always trampled grass inside the corner where two sidewalks meet but it grows to the concrete where its straight - folks are taking a short cut.

Below is:

flat (much more acute than the rest), hollow, convex, and V bevel. One could substitute any value for the final approach distance back from the edge, and unless the cross distance ("T" on your diagram) is a constraint the hollow will have the least material, convex next, V bevel will have the most. Remove "T" and the initiation point for the convex arc is free to move closer to the spine, shrinking the enclosed area.

Entirely possible Gillette uses a convex to improve initial penetration, lower friction and wedging forces as it cuts into the whisker...

 

[chiral.grolim]

I am still not clear on why the convex would be thicker than any flat sided approach until one reaches a straight line.

It must be by definition of the word "convex".

Remove "T" and the initiation point for the convex arc is free to move closer to the spine, shrinking the enclosed area.

The 'T' is arbitrary, put it ANYWHERE and the results are the same, the flat bevel will fit beneath it. Again, that is what the term "convex" means. And your diagram is comparing a bunch of random edges with variant geometries, what is its purpose??

Entirely possible Gillette uses a convex to improve initial penetration, lower friction and wedging forces as it cuts into the whisker...

EXACTLY the OPPOSITE. The convex reduces penetration and increases friction through wedging because it displaces more material as it proceeds. However, it is implemented because it also provides greater material support to prevent bending/flexing of a thinner flat-edge which, while possessing increased penetration and reduced friction, is more susceptible to deformation.

 

[HeavyHanded]

You haven't addressed the whole bridging between two joining planes issue.

The convex reduces penetration and increases friction through wedging because it displaces more material as it proceeds.

!!???
I can't add anything to that...