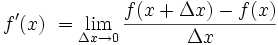Degree of Sharpness?

[Twindog]

That's the whole point...I never once claimed to compare V edges to convex edges. I was only showing that the theoretical terminal apex angle of a convex edge can be determined mathematically.

OK, cool. But there is no apex angle on a convex edge, there are two arcs that intersect. The angle you're referring to is the angle of the tangents of two intersecting circles, not the angle of the convex edge. Only two straight lines can form an angle. Convex edges have no straight lines.

 

[Fred.Rowe]

A convex edge has no angle -- only converging straight lines that meet at a vertex have an angle.
https://www.mathsisfun.com/definitions/angle.html

What you are measuring is the angle of two straight lines, in this case the tangents of two intersecting circles. The angle of the tangent (two straight lines) is not the angle of the convex edge formed by two intersecting arcs. As you can see, the tangents are outside of the convex edge at every point except the single point at a perfect apex. And no convex edge has a perfect apex, the angle of tangent doesn't even exist except in perfect theory. No single point can have an angle.

The two tangents in this case share a common point, and the angle of the tangent is good only for that single point, not any place on the actual edge bevel. If you go back from the apex on that edge by only a split whisker, you'll have two different tangents and a different angle of tangents. If you go back another whisker or so, you'll get two tangents with yet a different angle.

In fact, any convex edge has an infinite number of angles of tangent, each with a different angle. A V edge has a constant angle for the entire edge.

The problem is you can't directly compare a V edge to a convex edge. When you try to say a convex edge has an angle (or a angle proxy), you end up with a situation like trying to divide by zero.

Where you go wrong is saying that the angle of the tangent is the same as the angle of the convex edge. The convex edge has no angle. It has an infinite number of angles of tangent and all are different.

The solution to this is in the OP. The premise of the OP is as follows: By dividing the sum of the interior angles, that make up a given "V"edge by the sum of the angles that make up a given convex edge with a constant radius and using identical X-Y axis measurements, the result is a comparative proportion of sharpness between the convex edge and the "V" ground edge. The convex edge: the angles of deflection in degrees, minutes and seconds along the subtended curve, to a fine enough degree to offer accuracy of measurement. It helps if you make this edge 100 ft high instead of it being 1/16 of an inch high. It works when you compare a concave edge to either the convex or the flat "V" edge as well. The concave, since its inside the tangent of the flat edge will be considered a negative number. Fred

 

[Chris "Anagarika"]

Final angle on a convex is the one you form by height of spine vs the width of blade (spine - edge), regardless how small it is, against the stone when apexing the edge. That's what HH trying to say.
Theoritically you can't measure the real convex angle. Practically you can, by the way you sharpen (call it microbevel, etc.). I agree with him that by doing this, a convex has to be thinner anywhere behind the apex, than flat, because with same final apex angle, to make a convex, you have to lower the spine (remove material at lower angle).

 

[Fred.Rowe]

Final angle on a convex is the one you form by height of spine vs the width of blade (spine - edge), regardless how small it is, against the stone when apexing the edge. That's what HH trying to say.
Theoritically you can't measure the real convex angle. Practically you can, by the way you sharpen (call it microbevel, etc.). I agree with him that by doing this, a convex has to be thinner anywhere behind the apex, than flat, because with same final apex angle, to make a convex, you have to lower the spine (remove material at lower angle).

Not if you maintain the X Y measurements and that is not making an apples vs apples comparison. Your looking at apples and oranges. That apex angle is not actually measurable, where as if you maintain the geometry of the demo blade, the convex will always be outside the tangent of the "V" thats a given. If you use the equation I put forth the comparison is quite objective. I talk to Martin on a regular basis and understand this aspect of convex geometry.

 

[Gaston444]

The problem is you can't directly compare a V edge to a convex edge. When you try to say a convex edge has an angle (or a angle proxy), you end up with a situation like trying to divide by zero.

Maybe in theory you can't, but in practice all you have to do is define the lateral edge thickness at its base: For a given lateral thickness (which in large part determines the ultimate lateral edge strength), the v edge will always be thinner and sharper, below that point, than the convex edge...

One of the ideas of the convex edge advantage is similar to notions of "aerodynamic drag": Knocking down the corners, and at the same time get a shape that is more resistant to deformation, the closer you get to the thinnest end... This does make convex edges in theory more resistant to very small scale chipping...

In practice, for the same lateral edge base width, defined by the primary bevel top thickness on a v edge (and no, the convex edge doesn't get to choose whatever it wants, since it must match laterally for an objective overall strenght comparison), the v edge will always be sharper, as chiral.grolin correctly pointed out...

To say a convex edge "has no angle" is pure rhetoric: There comes a point where the practical differences amount to nothing... Or to saying it has no sharpness at all either...

I don't know if convex edges have actual practical advantages on knives (they may), but since they can't easily be applied in the field, I've always understood them as a knifemaker-driven idea, rather than a user-driven idea...

Gaston

 

[Chris "Anagarika"]

Fred,

I'm not disputing the theory. In practice, when sharpening final touch up angle is what counts. Your way of measurement gives us numbers for something we've been seeing but yet quantified.
If X & Y are constant, flat and hollow is always sharper. No doubt about it.

However, I can't control that when sharpening. I can only control how obtuse the final apex is. The rest is either same (flat) or thinner by removing material at shoulder. I don't have wheel, so I definitely can't produce hollow.

Unless I consciously choose a thicker convex that is having more obtuse apex. Yes, it is not apple to apple as in real life, I can't ensure X & Y constant. The best I can do is make sure spine height is constant when apexing.

We're actually saying the same thing but from different way of elaboration.

 

[bpeezer]

OK, cool. But there is no apex angle on a convex edge, there are two arcs that intersect. The angle you're referring to is the angle of the tangents of two intersecting circles, not the angle of the convex edge. Only two straight lines can form an angle. Convex edges have no straight lines.

The angle of intersection between two curves is well recognized as the angle between the tangents at the point of intersection.

http://en.wikipedia.org/wiki/Angle#Angles_between_curves

The angle between a line and a curve (mixed angle) or between two intersecting curves (curvilinear angle) is defined to be the angle between the tangents at the point of intersection.

http://www.solitaryroad.com/c360.html

The angle of intersection of two curves is defined as the angle between the tangents to the curves at their point of intersection.

http://www.sunshinemaths.com/topics/calculus/angle-between-two-curves/

In order to measure the angle between two curves, we measure the angle between the tangents to the curves at that point.

http://www.pinkmonkey.com/studyguides/subjects/calc/chap5/c0505201.asp

Angle between two curves is the angle between two tangents lines drawn to the two curves at their point of intersection.

 

[HeavyHanded]

Final angle on a convex is the one you form by height of spine vs the width of blade (spine - edge), regardless how small it is, against the stone when apexing the edge. That's what HH trying to say.
Theoritically you can't measure the real convex angle. Practically you can, by the way you sharpen (call it microbevel, etc.). I agree with him that by doing this, a convex has to be thinner anywhere behind the apex, than flat, because with same final apex angle, to make a convex, you have to lower the spine (remove material at lower angle).

Chris, I cannot state it any better than this even with multiple diagrams and way too much of my hot air.

As an extreme I can point to my Bark River Necker that is a true full convex for half the edge from spine to apex. Is nearly a FFG and in use needs to be applied with some thought or the edge will collapse from lateral forces. To practically convert to a flat plane leading in one would have to turn it into a FFG with microbevel. Slight lowering of the spine would still "melt" the last bit. At that scale human error alone would turn it back into a convex but again - is just more hot air. Tit for tat till there is a single plane and final working angle is lost to the primary with both grind types losing the original angle, so in a mathematical sense it just spirals down into infinity and neither is "thinner" than the other.

At practical scale with edges that can be maintained without complex equipment is a little different - if there is an intersection of planes they can always be bridged by an arc. True, one can then describe a straight line within the arc point to point, but a practical amount of the original working angle must be left - something I find the convex can manage more readily than a series of flat planes.

In practice, better convex edges do not arc all the way to the edge, they become flat at the final approach and are only convex leading in. Either a series of parabolic arcs, or a single parabola that is so large, functionally it is flat at the edge.

Only if you fix dimensions does the convex perform as per the OP or many of the other suppositions, as Fred says apples to apples. Apples to oranges leaves us in math freefall to unrealistic scales.

 

[Fred.Rowe]

Fred,

I'm not disputing the theory. In practice, when sharpening final touch up angle is what counts. Your way of measurement gives us numbers for something we've been seeing but yet quantified.
If X & Y are constant, flat and hollow is always sharper. No doubt about it.

However, I can't control that when sharpening. I can only control how obtuse the final apex is. The rest is either same (flat) or thinner by removing material at shoulder. I don't have wheel, so I definitely can't produce hollow.

Unless I consciously choose a thicker convex that is having more obtuse apex. Yes, it is not apple to apple as in real life, I can't ensure X & Y constant. The best I can do is make sure spine height is constant when apexing.

We're actually saying the same thing but from different way of elaboration.

I quite agree. My OP is not something used in real world sharpening. I would never lay out the curve of a convex edge and then transfer it to the edge of a blade. I, as a surveyor and having an engineering mind only wanted to share what I thought was an interesting mathematical comparison. In truth, I know it points out the obvious, overlaying a convex on the profile of a flat "v" edge, the "V" will always be thinner; I don't know if everyone picked up on the "equation" of comparing the degree sums of one shape to other shapes. For those that did, I think this reality is useful when considering different edge profiles. I know it has helped me. I'm a bit of the odd duck in that I grind primary bevels using fairly exact angles and then follow that by grinding fairly exact edges on those primary bevels.
I couple of years back I posted a thread that ask of knife purchasers and users " would find it useful if the knives you purchased contained the edge specifics, what the sharpening angles of the edge is and what process is best used to maintain the edge" you would have thought I'd dropped a dead cat in the midst of polite conversation. I had several very well known high end makers that posted, I have no idea what the edge angles are. That shocked me.

Anyhow, an interesting discussion and one for the most part did not place one edge in competition with another, which in my mind is a useless exercise.

Thanks for posting, Fred

 

[Twindog]

If you look at Bpeezer's diagram, you'll see what could be a convex edge, at least from at the apex to the 0.650 width line. If I understand Bpeezer correctly, he is saying that the angle of the tangents (green lines shown by the blue line to have an inclusive angle of 77 degrees) as being the way we measure the "angle of a convex edge." Actually, angles can be measured only by straight lines, which is what the diagram is doing.

But the key point is looking at the V edge at 77 degrees compared to the convex edge that has an angle of tangents of 77 degrees. The convex edge is more acute than the V edge at every single point on the edge bevel, other than a single point at the apex. To say that Bpeezer's V edge at 77 degrees has the same acuteness as the convex edge with an angle of tangents also equal to 77 degrees, is clearly not the case.

In the OP, Fred states "I don't know of a way to measure the actual curve of a convex edge..." That's really the key point.

Lets say that I and a friend each get a new Spyderco Military with uneven, rather obtuse edge bevels. I get out my Wicked Edge and put on a 30-degree inclusive edge bevel taken to 1600 grit. I tell my friend how much better my knife now cuts. He could easily reproduce my V edge to get the same results.

But if I said I convexed my Military edge and got a great improvement in performance, my friend would not have enough information to reproduce that edge. And I don't have the measurement skills to tell him. That's the problem with convex edges. None of us can describe them with the precision that we can a V edge.

People on the forum keep talking up how great convex edges are, but those comments are meaningless. A convex edge can be tall or short, acute or obtuse. It can be a product of perfect circle radii, as Bepeezer's chart, or it could be a blend of arcs. And the convex edge could be, for all practical purposes, identical to a V edge. Or it could be a hybrid of a convex and V edge.

Someone above said it doesn't matter if convex edges can't be measured because arcs to not meet to form angles. But it does matter, because unless we can describe what the convex edge looks like, we can't replicate it. Convex edges can cut well or cut poorly. It all depends on the geometry. V edges are easy to describe, but we can't do the same with convex edges. And convex edges are not all alike.

 

[bpeezer]

If I understand Bpeezer correctly, he is saying that the angle of the tangents (green lines shown by the blue line to have an inclusive angle of 77 degrees) as being the way we measure the "angle of a convex edge."

That's not what I'm trying to say, but my point is such a small aspect of the overall discussion that I won't pursue it further.

 

[HeavyHanded]

It really isn't that tough to describe a convex with a fair amount of accuracy, but it cannot be done with absolute accuracy. In all reality, unless one is using an EP or similar it isn't possible to describe the V bevel with absolute accuracy either.

We can describe with reasonable accuracy the final angle of approach from shoulder to apex. We can describe with accuracy the primary grind. If we then cut off the shoulder of the V bevel at a spec'd angle, to a spec'd depth (width of bevel that eliminates the shoulder), we have established the convex with a great deal of accuracy. All that is now required is to blend the two shoulders into the primary, the newly created flat, and the final cutting bevel. If we spec the distance each will be ground it gets even more accurate.

True, this is a lot of rigamarole, but will also make a very accurate convex defined by the three flat planes that act as reference/anchor points.

Would be far easier to simply say that if we have a primary at such and so angle, and a cutting bevel at another, and simply grind the shoulder into both planes it will turn out very comparable. This goes back to the premise that a convex must have an arc to the apex, but it really doesn't nor should it.

 

[chiral.grolim]

That's the problem, you should not measure the tangent. You should measure the thing that can be measured (the bevel), calculate the curvature of the bevel, then calculate the tangent at the relevant point (the apex).

I was able to redo this on Inventor, here is an image of the Gillette example.

Not "should not", you CANNOT measure the tangent, it doesn't exist, it is purely theoretical and impossible in reality. A "tangent" can only just touch the curve, meeting it at a single point, a "point" being utterly dimensionless = theoretical, not real. To use the wikipedia description:

The intuitive notion that a tangent line "touches" a curve can be made more explicit by considering the sequence of straight lines (secant lines) passing through two points, A and B, those that lie on the function curve. The tangent at A is the limit when point B approximates or tends to A. The existence and uniqueness of the tangent line depends on a certain type of mathematical smoothness, known as "differentiability." For example, if two circular arcs meet at a sharp point (a vertex) then there is no uniquely defined tangent at the vertex because the limit of the progression of secant lines depends on the direction in which "point B" approaches the vertex.

It has already been made clear that curves do not have "angles" per-say, angles are only achieved between straight lines, hence the need to derive a tangent (a straight line) with a defined slope (i.e. angle) through a complex mathematical equation, the derivative which I presented earlier:

It seems that any individual describing convex as "thinner than flat" understands neither English nor Math, and I am an expert of neither. In English, convex means to curve "out from" the associated flat, so any flat than the curve does NOT curve "out from" is NOT the associated flat. To HH, you are not "cheating" by drawing another line beneath the flat line, you are failing to grasp the definition of the word "convex" itself.

To clarify the math aspect, the ONLY way to accurately describe the angle of a convex edge IS by measuring the bevel's height and thickness and calculating as I already presented numerous times.

Why is this the only way? 1) the definition of the term "convex", and 2) the real-world limitations of "limits" via mathematical derivatives.

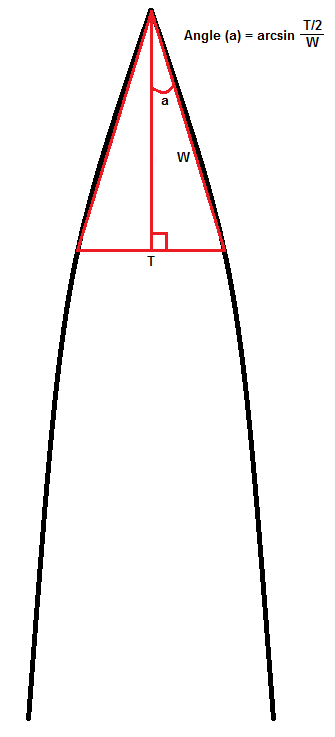
bpeezer has graciously plugged a series of measurements into a computer program which extrapolates a "best-fit" curve to the data points, generating an equation of the curve (a mathematical function) and deriving therefrom the radius of curvature as well as the limit of a secant-line through points A & B which lay upon that curve ('W' in my diagram), the line necessarily passing beneath (thinner than) the curve. Understand that the tangent thus derived does not lay "above" the curve, it resides ON the curve at the point selected. *****In relation to the tangent line, the curve is NOT "convex" at all as it does not meet the definition.***** The curve is only "convex" relative to the length 'W' between points A & B.
HOWEVER, the way in which the tangent line is arrived at, the derivation, depends entirely on how close to the apex the measurements of thickness were taken, i.e. the measurement of bevel height and thickness, essentially the 'T' and 'W' presented in my diagram - and I use 'W' as the length of the hypotenuse (bevel width) because one cannot practically measure the other length without taking a cross-section and so damaging the blade, it is an interior measurement whereas the bevel width is exterior and simple to measure.

'T' is relative to where 'W' is measured, and the tangent is derived from making 'W' as short as possible. 'T' and 'W' MUST BE FIXED measurements to derive the tangent of the curve, they are the data points. Cutting a NEW bevel that curves beneath W meeting only at the apex simply creates a NEW 'W' to be measured, hence why HH's method fails to grasp reality. Now in order for bpeezer's software to generate a best-fit equation, he required not just one 'W' and 'T' but multiple (at least three) heights and thicknesses of measurable dimensions to input into the software. What if he'd had only one set, one 'T' and 'W', e.g. 0.4 microns back 0.25 from the apex? The data is insufficient for the software to generate a curve with any degree of accuracy. As I already pointed out, taking into account the reality of limitations in apex size using steel, the angle of that first bevel is 33.7 degrees per side - in front of that bevel, the steel rounds over to an apex of 90-dps with a diameter ~0.2 microns. Which is the "terminal angle" or even the "working angle" of the blade edge, the apex or the angle behind it? Or the angle behind that? Or the one behind that?? Just like the relative importance of the primary bevel angle to the edge angle, the answer depends on the material being cut and depth of penetration.

Backing up, bpeezer ignored the apex-reality and used three measurements behind it to generate, via software, an equation that could produce a tangent at the apex of 38.7 dps. I ignored the apex and used ONLY that first measurement, did NOT generate a curve via software analysis (which I lack), and achieved almost the same exact angle! How is that possible? Because the software guesses at thicknesses 'T' and bevel heights 'W' that have not or cannot be measured due to practical limitations, it produces straight secant lines falling beneath the curve with immeasurably small lengths 'W' and relying upon the equation generated also guesses immeasurably small thicknesses 'T' until it achieves a 'W' and a 'T' that are essentially without lengths, only position and gives the slope of the line generated by a straight secant beneath the curve one immeasurable step back from that.

Understand what I just told you? As previously stated, a 'point' where a tangent touches has no dimensions and so can present NO "angle" or slope for the tangent to possess, but TWO POINTS form a secant-line beneath the curve (which allows it to be called "convex" in relation to that secant) and so present a slope and angle. How long is that secant-line 'W'? For the software, it is immeasurably short since adjacent two-points are infinitesimally close so as to be indistinguishable except in mathematical fairy-land of the imagination. In the real-world, by using the smallest set of measurements available and producing a secant-line to the apex, we are not achieving the theoretical limit of the angle as described by the tangent because it does not exist, but present an approximation of the "working angle" in the only reliable real-world method available.

To HH, your of undercutting my 'W' with yet another curve fails utterly because the equation of THAT curve requires new measurements and new secant-lines to approximate a NEW bevel angle. It does NOT in any way maintain the same "working angle" or "terminal angle" or whatever other term you may select to try to describe it. The "chase" you describe ONLY happens if you keep cutting new curves, which isn't necessary.

Now I read that many admit to only cutting off the shoulders of bevel-transitions and not actually curving all the way to the apex such that the approach to the apex is as flat as possible, whereupon the reality of my argument is even more obvious. By cutting down the shoulders, you create NEW transition bevels whose curvature can only be determined through flat-line measurements, just as Archimedes inscribed polygons in a circle to approximate the value of Pi.


Hopefully this is my last post on the topic, but i encourage all to recognize the definition of the word "convex" and the process of mathematically deriving the "angle" of a curve which relies heavily upon that definition being "curving outward from flat" - if the definition did NOT demand that convex being ALWAYS thicker than flat, the process of deriving a tangent at all would be impossible.

 

[Gaston444]

You are right chiral.grolim, but I doubt they will accept it...

The funny thing about convex edges is that they are such a late 20th century idea... Nobody who actually depended on blades (a lot more than we do), throughout history, has ever even considered the idea of making a convex edge (except on wood axes maybe)... At least as far as I know: I first heard of them as largely a Bill Moran idea from the 1970s...

If I want a blade really sharp, I will flatten a curve...

Gaston

 

[Fred.Rowe]

I think this has run it's course.

Thanks for all the input. I hope my original comments regarding a different perspective on how we view different cutting edges is food for thought.

Best Regards, Fred