Ok ..... next little nibble. Keep in mind that energy (heat) always flows from areas of high temperature to areas of low temperature - the reasons for this follow from statistical mechanics (which we dont want to go in to here) .... but should make pretty much intuitive sense. So .... "heat" (or a roughly equivalent term "energy" - but I will stick with "heat") is NOT the same at temperature - the two being related by the "heat capacity" of a material, which I will mention, but not spend a lot of time on here.
Also, I lied - I do need to use an equation or two (simple one though). The heat transport equation that describes the movement of energy through an insulating wall, at any infinitessimally thin "slice" on the inside of the wall is:
Q = - k * dT/dx, where is the amount of heat energy moving through an area of unit area, k is the thermal conductivity of the material, and dT/dx is the temperature gradient (the
slope of the temperature curve from inside of the oven to the outside wall). the negative sign is there so that the heat flux is a positive value (because the slope of the temperature is negative - remember, heat moving from areas of high temp to areas of low temp). remember, this equation holds independently at every location through the thickness of the wall.
In words:
heat flux through a segment of wall of area "1",
at any location or depth in the wall, = thermal conductivity
multiplied by the
local change in temperature versus distance towards the outside of the wall.
if that is understandable, then you might think that the slope of the temperature curve at different depths in the wall can be different. BUT, again we are considering "steady state" here .... and an important thing to keep in mind is that, to avoid energy being created or destroyed (which it can not), t
he heat flux at every location in the wall has the be exactly the same as every other location in the wall. so "Q" (the local heat flux), must be some fraction of the energy put in by the heating element on the inside of the oven. for convenience - I will assume all the energy put in by the heating element goes through a single unit area .... so I will just say that Q is the same as the power of the heating element.
Because the energy put in by the heating element does not change, and (we assume here) that the thermal conductivity does not change with wall depth, then at every "depth slice" through the wall, flux is constant, the heat capacity is constant, and so the temperature gradient must be constant at all locations through the wall (it is constant).
By the equation, Q = - k * dT/dx, if Q is constant, and K is constant, then dT/dx
must also be constant.
Also, if you have a bigger heating element, then the heat flux through the wall must be bigger (must be the same as the input of the heating element), and if the thermal conductivity is constant, then the gradient of temperature through the wall must be bigger.
by the equation Q = - k * dT/dx, if Q is bigger, and if k is constant, then dT/dx
must be larger.
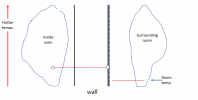
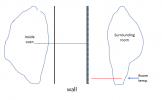
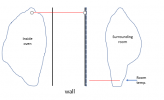
If I have not lost you in the above, then we can look at that with a picture. Assume a situation where instead of perfectly insulating the outside wall of the oven, you find a way to absolutely pin the temperature there right at room temperature (say, blowing a really strong fan over the wall, or putting the oven in a water bath (dont try that for real), or by putting a cooling plate on the outside with room temperature water flowing through it....), then you have a situation like the below (it is important to remember here that the slopes of the temperature lines are defined by the power of the heating element,
not by the fact that the temperature of the oven is higher (the inside temp is defined from the slopes and the starting known temperature on the outside):
View attachment 1483535
All the above essentially explains why, all else being equal, when you use a higher power heating element, the inside temperature of the the oven
must be higher than if you used a lower power heating element (here we are assuming that the heating element is going full-bore - 100% output all the time). Starting with the known temperature on the outside of the oven, the higher slope of the temperature curve(which is required when the heat flux is higher)
must result in a higher temperature inside the oven.
This is still a pretty simplified and idealized view of the thing, but is meant to try to give intuition as to how the different parts of the system interact and affect each other. Let me know if/when you have digested this .... and when we have gotten there I can move on to more complicated situations - like when you are not explicitly controlling the outside temperature of the oven....
Oh ..... "extra credit"

. From the above, if you have the same power heating element, walls with the same thermal conductivity, BUT the wall is twice as thick - can you see why the temperature of the inside of the oven must be still higher yet?