Diy heat treat oven help

[Drew Riley]

Want to take a stab at the extra credit? If you can explain that, then you basically do get it...

Sure... assuming Q (red line) is constant, and the outer (room) temp is constant, then it’s basic trig. Q can be the hypotenuse (call it “c”. Wall thickness would be “a” and the difference from outside and inside temps “b”. Thanks to Pythagoras, I know that increasing “a” must also increase “b” and “c”.

At least, that’s how it can be viewed from the example above.

 

[Cushing H.]

Bingo . Keep thinking that way. Understanding that the heat flow and the temperature gradient in the wall are so strongly related is the key to everything else....

 

[Cushing H.]

ok .... so now that you got that .... lets move closer to the real world. If we take the oven out of the water bath ( )Once the oven heats up (and while it heats up) the outside of the oven will want to get warmer or hot. Once everything has settled down and everything is at its final temperature ("steady state"), per the previous discussion, the total heat leaving the outside wall of the oven MUST equal the total heat put into the chamber by the heating element. (I will talk more later about what happens when things are not steady - i.e. "transient", but not now). Anyway - there are three mechanisms for heat to leave the outside wall of the oven and escape into the bigger environment around it:

1. conduction (like how heat moves through a solid like metal or insulating bricks)
2. convection (air moves over the outside wall of the oven, picks up heat from direct contact, then gets swirled away by air currents (natural or fan driven)
3. radiation (like when you put your hand in front of something hot, and you feel the heat from the thing on the palm of your hand).

Air is really a pretty bad conductor - which is the very reason most insulators work so well - the small spaces in fiberglass or the pores of firebrick are so small they do not allow convection - only conduction through the air in the pore ..... but again still air is a bad conductor - hence the insulating properties of firebrick with small pores in it. so.... loss by conduction is a rather minor player from the outside of the oven.

radiation is hands down the heat loss mechanism with the greatest potential to move heat (think about feeling the heat of the sun on a clear summer day - yet there is no air in space. all the energy reaching you does so by radiation. BUT - radiation only becomes really important at rather high temperatures - pretty much above the temperature you would ever want the outside of the oven to reach. So, like conduction, radiation is a pretty small player in the loss of heat from the outside of the oven.

that leaves convection (which is what JT was getting at). For the most part people do not put a fan blowing over the outside of their oven. Instead (again, like JT talked about) - the air immediately next to the outside wall of the oven heats up, then the buoyancy of the hot air causes it to rise (like the hot air in a balloon lifts the balloon and gondola up to great heights). that rising air carries the heat up into the greater room and away from the oven. Because something needs to replace the air that rose upwards, colder air is drawn up from below, gets warmed in turn by contact with the hot wall, rises upwards, etc, etc. Convection can be a really effective way of moving heat away from something.

Here is an important point: the efficiency of heat transported by natural convection increases as the temperature of the wall goes up (because the heated air rises faster, and carries greater volumes per unit time of cold air in to replace it. on the other hand, When the wall is cooler, heat loss by convection is not very good at all.

EDIT - I forgot to add this. Engineers will describe this convective loss of heat by a really simple equation:

heat loss = C * (Twall - Troom)

where Twall is the temperature of the wall, Troom is the temperature of the greater room, and "C" is a "heat transfer coefficient". With convection, the value of C is incredibly hard to predict (and changes with temperature!) - and the engineering handbooks devote a lot of space to tables, charts, and graphs - but they are still mostly only estimates except under very simple and constrained conditions. For purposes here, lets just stick with the simple statement that "the rate of heat transfer from the wall increases as the temperature of the wall goes up....

I'll talk about the implication of that in a post immediately after this one...

 

[Cushing H.]

Drew - I edited the previous post - might want to re-read it.

So .... for this discussion I am going to talk about what happens as the oven and the wall heat up. In reality, during this stage, the temperature profile of the wall is NOT linear .... but here I will portray it as linear just to not confuse the real point (again .... this is a "pseudo steady state assumption". ) Ok .... so lets take a situation where we turn on a cold oven with a heating element going full bore, putting heat into the oven at a rate of "Q". A little while later, the outside of the oven has warmed up a little, but not enough to cause the convective loss to the outside to be the same as the input of Q by the heating element. The difference (input of Q versus the smaller loss to the outside room) just goes to heating up the material of the wall (temperature rise of a material equals heat input to the material by a property called "heat capacity" - the greater the heat capacity the smaller the temperature rise for a given amount of heat put into it).


And so .... as the element continues to pump in heat at a rate of Q, the temperature of the oven and the surrounding walls continue to rise. At a later time, the situation might look like this:

The temperature of everything has risen, but convection from the outside of the wall still has not take off yet .... an so even though the heat loss from the outside wall is faster than in the first picture, it STILL is not the same as the rate of Q put in by the heating element (by the equation - (heat loss = C * deltaT) the convective heat loss coefficient still is somewhat small, AND the value of deltaT (the difference between the wall temp and the room temp) are both small, an so heat loss is small). And so the temperature of the oven continues to rise..... eventually the temperature of the outside wall reaches a point where loss of heat by convection is equal to the value of Q of heat put into the chamber by the heating element.....

In this situation, the wall is heated up to where it is going to get to (what you would call "fully soaked"), and so no energy from the element goes into heating up the wall any further. The same amount of energy Q that goes into the chamber by the element travels through the wall from inside to outsid (that rate defined by the slope of the temperature curve), and that same amount of energy, Q leaves the outside wall and escapes into the room. Think of this as a stable "balance point". If for some reason the outside wall cools off (you blow on it or spill water on it), the loss by convection decreases, and heat would accumulate in the wall until the convective loss again is the same as the input Q. On the other hand .... you were to somehow heat up the outside wall, convective losses would go up, causing the wall to cool off, until it reaches back to that balance point.

Here is another fairly important point: if you were to somehow change that outside temperature that creates equilibrium (say by raising the room temperature considerably) .... remember, the heat loss from the outside wall STILL has to be equal to the input Q by the element - that value of Q again predetermining the slope of the temperature curve in the wall (because the heat flux through the wall HAS to still equal Q). That situation looks like this (where the dashed temperature lines indicate the "new" situation:

Note that the temperature inside the oven must rise by some amount, because ultimately everything is connected, and you can not get away from the requirement that input Q MUST be the same as the output Q.

If you make the walls twice as thick (but keep the thermal conductivity the same), then - the "equilibrium" temperature of the outside of the oven does not change, the slope of the temperature curve through the wall does not change, so, by the same argument you applied last night, the temperature of the inside of the oven MUST increase (even with the same value of Q coming out of the element.

If all of that continues to make sense, then I can move on to three other things I think I should touch on: what happens with walls with different thermal conductivity, what happens when you are controlling the inside temperature with a PID controller, and how do we get away from this simple geometry and think more about the actual shape of the oven - which if you think about it is more of a sphere than the simple plane above, and has an outside surface which is much bigger than the inside surface of the inner chamber....

 

[Drew Riley]

I don’t know about anyone else, but I’m getting a lot out of this. Much appreciated.

 

[Cushing H.]

I don’t know about anyone else, but I’m getting a lot out of this. Much appreciated.

Well ... I guess this is just another way to think about the ovens ... more analytical ... driving to understand why they behave the way they do. People out there who say this does not change the design / build guidance out there are absolutely right. It all depends on personal preference.

although, I was thinking last night that this is just about at the point of being able to clearly point out where and why the oven behavior described by the OP that started the process bread is “weird” and confusing. ... as what is seen is not what would be expected ... even for an oven with low power / low insulation...

 

[Cushing H.]

So now I think I want to change things up a bit. In the past I have been talking about cases where the heating element inside the oven is just blasting away at its full output, and trying to give insight on how the temperature of the oven settles in on a certain temperature, and why that temperature might be too low (because the outside wall is allowed to get hot enough that the loss of heat there is equal to the full output of the heating element .... and so the heating element just cant keep up enough to raise the temperature any further.

So .... lets start talking about insulation. so far I have said lets consider the thermal conductivity of the in wall is constant, and said that a greater temperature gradient in the wall coincided with a greater heat flow through the wall (which was convenient at the time). But .... lets go back to that equation, and instead ask - if for a given value of Q (heat input from the heating element) - how does a changing thermal conductivity affect the temperature gradient. so starting with:

Q = - k * dT/dx

Do just a little bit of algebra to get:

dT/dx = -Q / k

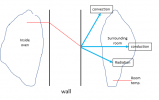
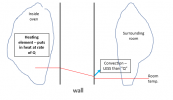
IN other words, if the wall is a better insulator (thermal conductivity k is smaller), then for a given value of Q (heat input from the heating element) the temperature gradient in the wall is BIGGER. This is how we intuitively think about how insulation works: when it is cold outside your house, good insulation in the walls keeps the inside walls nice and warm. So, as an intermediate step, lets go back to an earlier diagram where we were able to "magically" fix the outside temperature of the wall at room temperature .... but instead visualize how the changing thermal conductivity of the wall affects the temperature profile in the wall for the case where the heat input from the heating element, Q, is constant:


So ... even though we now loose the "temperature slope is proportional to the heat flux Q" .... this still kind of makes intuitive sense: a poorer insulation in the wall gives rise to a lower temperature inside the oven (again, the heating element is running full tilt ... .and if the heating element is not strong enough, then the temperature inside the oven can not get hot enough).

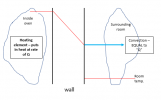
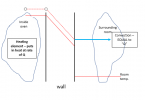
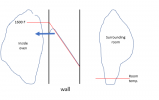
But now .... and Im sorry about this .... I need to add what might be the most confusing thing about this. NOW, lets take the case where we fix the outside temperature at room temperature, And we use a heating element with power sufficient to overcome the bad insulation in the wall, AND we use a PID to control the inside temperature of the oven, say to 1600F. This situation looks visually like this:


So what should look weird about this is that for very different wall thermal conductivities, the temperature slope in the wall is the same. How can that be given everything I said before???? Well .... look again at the diagram above, and note that I have not said anything about fixing Q. In this case, we have fixed the value of the temperature gradient dT/dx by using the PID to pin the inside temperature, and have also said we are magically controlling the outside temperature to be room temperature. We have also said we are defining the value of K (thermal conductivity). Now Go back to the equation for heat flux through the wall:

dT/dx = -Q / k

The only way for dT/dx to be unchanged as k is varied is for Q to change (Q is bigger for larger k, and smaller if k is smaller - i.e. the ratio between Q and k has to be unchanged.). Although you will not see it unless you look closely at your oven running - this is taken care of by your PID! If thermal conductivity is large (large k / poor insulator), then the PID will cycle the heating element on more often. if the thermal conductivity is small (small k / good insulator), then the PID will cycle the heating element on infrequently. sorry - in this case you just need to do the math to see where the heat flux Q settles.

This is why I tend to really like "thought experiments" - they get away from the math. For example, for a really, really efficient insulating wall (like my earlier 100 mile thick wall), once the inside of the oven is up to temperature - even though you still have that temperature gradient in the wall - heat loss through the wall to the outside is really, really small - and the heating element basically needs to put zero heat into the oven for the temperature there to say basically constant (this is - after all - exactly how a really good vacuum thermos works to keep your coffee hot!).

In these cases of thick walls / small values of thermal conductivity - a powerful heating element is useful for getting the oven up to temperature quickly - but are not needed to maintain the temperature once it has been reached. But remember .... for steady state (fully soaked) conditions, we did not, and never will loose, the requirement that the heat input from the heating element, Q, must be the same as the total heat lost from the outside of the oven.

Please let me know affirmatively if this makes sense, or whether I have completely lost you. Because ... the next (and I think second to last) step is to bring back convective loss at the outside of the oven and allow the temperature there to change and settle in on where it needs to be for Q to be constant everywhere.....

 

[Drew Riley]

Please let me know affirmatively if this makes sense, or whether I have completely lost you.

Yes, it does make sense.

 

[JTknives]

This has been a good thread I think.

 

[Cushing H.]

thanks JT ..... hopefully you do find something useful/insightful in all of this. I had no time today to try to finish this up. will try again tomorrow....

 

[Cushing H.]

Ok .... I think I can do this kind of quickly. This time .... EVERYTHING floats. we are controlling the temperature of the chamber at 1600F, BUT we do not know how often the PID will cycle the element, so we do not know what Q (input) will be. Likewise, we are not fixing the temperature of the outside wall, but allow convective loss of heat to occur there. we will talk about two cases - one with not so good insulation (higher thermal conductivity), and better insulation (smaller thermal conductivity). Lets take the case of bad insulation (larger k) first:

the insulation is not so good .... so remember the stupid math says the slope of the temperature profile through the wall is smaller - which means the outside wall is hotter. we are controlling the temperature on the inside of the oven .... so what happens if something goes on to make the outside wall cool a little from where it "should" be (this can be a breeze, your soft drink spilling on it .... or the tail end of the heat up cycle...). In this case the cooler outside wall temperature implies a somewhat greater slope of the temperature profile through the wall. that greater slope causes/forces heat to be sucked out of the element chamber faster (yes really - remember the temperature gradient DRIVES the heat movement). this causes the heating element to cycle on faster (to keep at the set point) .... so the heat input to the oven (call it Q-input) goes UP. BUT on the other side of the wall, the temperature of the outside wall has gone down, so the heat loss to the outside world (call it Q-output) goes DOWN. the two are NOT equal and non in balance .... BUT that heat that got sucked out of the chamber flows down that temperature gradient .... causing the temperature of the outside wall to go UP. Eventually this "dance" reaches a balance where Q-input is equal to Q-output ... and there things stay. The opposite happens if the temperature of the outside wall increases somewhat. This is shown visually and with words in the graphic below:


With a case of GOOD insulation (lower k), things look exactly the same, except that, as we discussed above) the overall slope of the temperature curve through the wall is larger (and thus the temperature of the outside wall is cooler, and Q-input is smaller at equilibrium than for the bad insulation case:

but after the oven heats up, and everything is at its equilibrium "balance point" ... you dont see that minutia (even though those details are driving what you see in terms of temperature inside and outside of the oven. What you DO see is that in the case of the bad insulation, the outside wall is hotter, and in the case of the good insulation (lower thermal conductivity) the outside wall is cooler. (for equal thermal conductivity, you can substitute "thicker walls" for "better insulation", per the trigonometry argument that Drew pulled out a few days ago):



IF YOU LOOKED MORE CLOSELY .... you would see that in the case of the bad insulation (larger thermal conductivity), the heating element would be cycling more often (in which case the overall steady state heat flux Q would be larger than in the case of the good insulation).

this gets to why the original observation of the OP that his oven did not come up to temperature, but the outside walls did not get really hot is "weird": for bad insulation, if the heating element is not powerful enough to pump out the required larger value of Q-input, then the heating element would be on full-bore, but the inside of the oven would never get up to the set point. BUT .... per the above, in this case you would expect the outside of the oven to get pretty hot .... because (at equilibrium) all that energy being pumped into the inside of the oven would need to also leave, with the same large value of Q from the outside wall .... which would require it to be pretty hot. ..... and that is what started this whole discussion

If that continues to make sense, I would like to pretty quickly touch on what things look like during the transient heat up ..... and then finish with how the actual brick-like geometry of a typical oven changes the above descriptions (but does NOT change the conclusions). Again .... hopefully all that continues to make sense....

 

[Drew Riley]

You're doing a very good job of explaining the concepts. You've definitely cleared up some misconceptions I had before all of this and things are making a lot more sense to me.

 

[Cushing H.]

Thought I would try to take a quick stab at transient / warm up. I am NOT going to try to make a description of what it happening inside the oven chamber itself - totally different discussion and totally different set of physics. for here, I will just take that perspective that as the turn the oven on, the chamber starts to warm up uniformly. so given that .... when you turn the heating elements on, the inner chamber starts to warm up .... and that starts to warm the oven wall .... the inner surface of the wall being essentially at the same temperature as the chamber itself. So, as time progresses, the temperature of the inner wall starts to go up, and that heat on the inner wall starts to penetrate into the insulating wall itself, heating the inner portion of the wall (remember, heat always flows down temperature gradients .... but that flow takes TIME (really defined by the thermal conductivity, k, of the wall. So .... you reach a point where the inner surface of the wall is warmed up quite a bit (but not at final temperature), BUT the outside wall is **just beginning** to heat up. that progresses over time, with the inner wall continuing to heat up, that heat continues to flow through the wall (with a chunk of that energy going to raising the temperature of the wall (because of its heat capacity), and another chunk of the heat not being "absorbed" by the wall, but continuing to flow down that temperature gradient towards the outer wall. ***if the insulation is good enough*** you could reach a point where the inner surface of the wall next to the chamber is essentially at your set point, and the outer surface is not yet warm at all (a really strong heating element could achieve this). In either case, as time goes on, the wall will continue to heat up until it reaches that steady-state linear temperature profile we have been discussing before. At that point, there is no more heat absorption/heating of the wall happening - and the frequency of cycling of the heating element by the PID will slow down to match the steady state heat flow through the wall (again, if the insulation is really good, then the heating element will only need to cycle on at a pretty low frequency). A more powerful heating element helps this progress towards a steady-state situation helps things get there faster because of two things: it makes more heat available to transfer to and heat up the material of the wall .... and by heating the inner chamber to higher temperatures faster it establishes higher temperature gradients in the wall, which in turn causes the heat to travel through the wall faster (again, remember heat moves faster with bigger temperature gradients)

Pictorially, this looks like this:


A couple points I would keep in mind. If you have a strong enough of a heating element, once the temperature of the chamber/inner wall reaches your set point (but the cross section of the wall is not fully heated), then you are good to go with your heat treating processes ..... with a couple caveats. When you open the door to place something into the chamber, AND the very act of putting something cold into the chamber, causes the temperature of the chamber and the very inner wall to cool down (thats because of that physics of the inner chamber I am not planning on discussing). So ..... how does the inner chamber heat back up??? Part of that comes from the heating element .... but a LOT of the heat that goes into re-heating the chamber actually comes from the portion of the wall immediately next to the inner wall. As the following picture tries to show .... when the door is open, the inner surface cools down, but there is a lot of heat in the wall itself that has not gone anywhere. Remember that heat flows down gradients from high temperature to lower temperatures. Well .... under these conditions, heat just goes ahead and flows down that temperature gradient from the hot layers of the wall, back towards the relatively cooler inner surface of the wall, and thus on into the chamber itself, helping to heat it back up (this flow is shown by the heavy blue arrow in the diagram below). This re-heating of the inner chamber is most effective when the wall is fully saturated (it contains more heat) and that steady state linear temperature profile is established.....

 

[DAMNENG]

I have the oven running now with the element wired directly to the power
15min 1020f
30min 1195f
45min 1335
60min 1430f
I also put a second tc in the oven on the floor temps were close

TZ Im jumping in a little late, so please forgive me if I missed a post covering what I'm saying.

Observations:
1. I DON't see any kind of gasket on the door. A small crack can lead to enormous heat loss.

2. The outlet you show is a 120Vac 15 amp outlet. Rated at 80% continuous current is 12 amps. 120vac @6.8 ohms is over 17.5 amps.
Jim A

 

[Drew Riley]

Thought I would try to take a quick stab at transient / warm up. I am NOT going to try to make a description of what it happening inside the oven chamber itself - totally different discussion and totally different set of physics. for here, I will just take that perspective that as the turn the oven on, the chamber starts to warm up uniformly. so given that .... when you turn the heating elements on, the inner chamber starts to warm up .... and that starts to warm the oven wall .... the inner surface of the wall being essentially at the same temperature as the chamber itself. So, as time progresses, the temperature of the inner wall starts to go up, and that heat on the inner wall starts to penetrate into the insulating wall itself, heating the inner portion of the wall (remember, heat always flows down temperature gradients .... but that flow takes TIME (really defined by the thermal conductivity, k, of the wall. So .... you reach a point where the inner surface of the wall is warmed up quite a bit (but not at final temperature), BUT the outside wall is **just beginning** to heat up. that progresses over time, with the inner wall continuing to heat up, that heat continues to flow through the wall (with a chunk of that energy going to raising the temperature of the wall (because of its heat capacity), and another chunk of the heat not being "absorbed" by the wall, but continuing to flow down that temperature gradient towards the outer wall. ***if the insulation is good enough*** you could reach a point where the inner surface of the wall next to the chamber is essentially at your set point, and the outer surface is not yet warm at all (a really strong heating element could achieve this). In either case, as time goes on, the wall will continue to heat up until it reaches that steady-state linear temperature profile we have been discussing before. At that point, there is no more heat absorption/heating of the wall happening - and the frequency of cycling of the heating element by the PID will slow down to match the steady state heat flow through the wall (again, if the insulation is really good, then the heating element will only need to cycle on at a pretty low frequency). A more powerful heating element helps this progress towards a steady-state situation helps things get there faster because of two things: it makes more heat available to transfer to and heat up the material of the wall .... and by heating the inner chamber to higher temperatures faster it establishes higher temperature gradients in the wall, which in turn causes the heat to travel through the wall faster (again, remember heat moves faster with bigger temperature gradients)

Pictorially, this looks like this:
View attachment 1486883

A couple points I would keep in mind. If you have a strong enough of a heating element, once the temperature of the chamber/inner wall reaches your set point (but the cross section of the wall is not fully heated), then you are good to go with your heat treating processes ..... with a couple caveats. When you open the door to place something into the chamber, AND the very act of putting something cold into the chamber, causes the temperature of the chamber and the very inner wall to cool down (thats because of that physics of the inner chamber I am not planning on discussing). So ..... how does the inner chamber heat back up??? Part of that comes from the heating element .... but a LOT of the heat that goes into re-heating the chamber actually comes from the portion of the wall immediately next to the inner wall. As the following picture tries to show .... when the door is open, the inner surface cools down, but there is a lot of heat in the wall itself that has not gone anywhere. Remember that heat flows down gradients from high temperature to lower temperatures. Well .... under these conditions, heat just goes ahead and flows down that temperature gradient from the hot layers of the wall, back towards the relatively cooler inner surface of the wall, and thus on into the chamber itself, helping to heat it back up (this flow is shown by the heavy blue arrow in the diagram below). This re-heating of the inner chamber is most effective when the wall is fully saturated (it contains more heat) and that steady state linear temperature profile is established.....
View attachment 1486894

Another excellent post. I never previously considered that the heat already inside the bricks would contribute to heating the oven back up after the door was opened, then closed, but it makes a lot of sense. I'm curious if this contributes to my temperature overshooting a few degrees when I heat put my blades in, or open and close the door to take one out.

 

[Cushing H.]

Another excellent post. I never previously considered that the heat already inside the bricks would contribute to heating the oven back up after the door was opened, then closed, but it makes a lot of sense. I'm curious if this contributes to my temperature overshooting a few degrees when I heat put my blades in, or open and close the door to take one out.

Quite possibly. D**n ... do I really need to spend some time on radiative heat transfer inside the chamber? I tried that (with an unnamed member of the forum) ... and he almost did not speak to me for a while after

 

[Cushing H.]

Ok, then here is the last thing I wanted to comment on. Engineering equations are based on relatively established coordinate systems. The regular "cartesian" system, which just uses the mutually perpendicular x,y,z axes is one of the most common. Other coordinate systems are the cylindrical (which, well, looks like a cylinder), and the spherical (which looks like a beach ball). Typically the equations that describe the physics we have been talking about - in this case heat transfer - are just plain simpler and easier to understand, and usually easier to draw pictures to describe. Which is why, even though I did not say so, I used that coordinate system and the corresponding forms of the equations for the discussion above. BUT .... rarely in reality do the actual things we are trying to make predictions about exactly correspond to any one of these coordinate systems - so we make approximations and say something like "lets use this coordinate system to describe what we are talking about ". (aside - one of my professors was an avid marathon runner .... and when we were studying fluid mechanics and the drag that wind would put on things, he posed an exam question that asked "Prof XXX is running a marathon at a pace of 7 minute miles. What is the drag on him from air he is running through". The solution literally began with the statemement "lets approximate professor XXX as a cylinder standing vertically"! ).

So anyway, a heat treat oven is clearly not just a single wall. It is a chamber with walls on all sides, AND those vertical and horizontal and vertical walls MEET each other in the corners, forming a structure that "wraps around" the inner chamber. So ..... for a relatively thin wall, this structure "feels" more like a cylinder. For even thicker walls, you could argue that the things begins to more and more closely resemble a sphere.
BUT - that does not really change any of the conclusions or insights that I tried to give above. The difference between this stuff described in x,y,z coordinates versus either cylindrical or spherical coordinates is that the requirement of a linear and constant slope of the temperature gradient through the wall goes away. Instead, because the heat leaving the chamber diffuses out into continuously larger volumes of material (after all, as the radius of a sphere goes up the surface area of that sphere goes up) the temperature goes down faster and faster because that moving heat gets "diluted" into greater volumes of material. Technically, the temperature goes down as 1 divided by the radius at that point .... but visually it drops fast near the center, then levels out more and more towards the outside of the cylinder or sphere. But .... heat still flows down a temperature gradient, and in the case of spheres and cylinders the steady state profile is very well defined .... and the physics of heat loss at the outside walls still stay exactly the same as discussed above. So .... the only real difference is that for a sphere and a cylinder, the temperature of the outside walls would be lower (but not cold) than what you would predict from what I wrote above. All the same intuitions still apply.

Ok .... that is all I thought I would need to say to try to give intuition about what is happening with heat and insulation in a HT oven. Before I ask the question on whether you really want me to talk about what is happening inside the oven, I should check whether all of that was clear enough .... of if there is something I still need to clear up.... ???

 

[Drew Riley]

Ok, then here is the last thing I wanted to comment on. Engineering equations are based on relatively established coordinate systems. The regular "cartesian" system, which just uses the mutually perpendicular x,y,z axes is one of the most common. Other coordinate systems are the cylindrical (which, well, looks like a cylinder), and the spherical (which looks like a beach ball). Typically the equations that describe the physics we have been talking about - in this case heat transfer - are just plain simpler and easier to understand, and usually easier to draw pictures to describe. Which is why, even though I did not say so, I used that coordinate system and the corresponding forms of the equations for the discussion above. BUT .... rarely in reality do the actual things we are trying to make predictions about exactly correspond to any one of these coordinate systems - so we make approximations and say something like "lets use this coordinate system to describe what we are talking about ". (aside - one of my professors was an avid marathon runner .... and when we were studying fluid mechanics and the drag that wind would put on things, he posed an exam question that asked "Prof XXX is running a marathon at a pace of 7 minute miles. What is the drag on him from air he is running through". The solution literally began with the statemement "lets approximate professor XXX as a cylinder standing vertically"! ).

So anyway, a heat treat oven is clearly not just a single wall. It is a chamber with walls on all sides, AND those vertical and horizontal and vertical walls MEET each other in the corners, forming a structure that "wraps around" the inner chamber. So ..... for a relatively thin wall, this structure "feels" more like a cylinder. For even thicker walls, you could argue that the things begins to more and more closely resemble a sphere.
BUT - that does not really change any of the conclusions or insights that I tried to give above. The difference between this stuff described in x,y,z coordinates versus either cylindrical or spherical coordinates is that the requirement of a linear and constant slope of the temperature gradient through the wall goes away. Instead, because the heat leaving the chamber diffuses out into continuously larger volumes of material (after all, as the radius of a sphere goes up the surface area of that sphere goes up) the temperature goes down faster and faster because that moving heat gets "diluted" into greater volumes of material. Technically, the temperature goes down as 1 divided by the radius at that point .... but visually it drops fast near the center, then levels out more and more towards the outside of the cylinder or sphere. But .... heat still flows down a temperature gradient, and in the case of spheres and cylinders the steady state profile is very well defined .... and the physics of heat loss at the outside walls still stay exactly the same as discussed above. So .... the only real difference is that for a sphere and a cylinder, the temperature of the outside walls would be lower (but not cold) than what you would predict from what I wrote above. All the same intuitions still apply.

Ok .... that is all I thought I would need to say to try to give intuition about what is happening with heat and insulation in a HT oven. Before I ask the question on whether you really want me to talk about what is happening inside the oven, I should check whether all of that was clear enough .... of if there is something I still need to clear up.... ???

I can only speak for myself, but I think you did a great job of laying out the basics and simplifying things down into bite sized and understandable chunks. You definitely cleared up some misconceptions I had.
If you want to delve deeper into the inner workings of an oven, I'm personally all for it.

 

[Tom Zaccagnini]

TZ Im jumping in a little late, so please forgive me if I missed a post covering what I'm saying.

Observations:
1. I DON't see any kind of gasket on the door. A small crack can lead to enormous heat loss.
no gasket on door but i did rout the door bricks to set in, it's a pretty tight fit, but possible that is were I am losing heat.


2. The outlet you show is a 120Vac 15 amp outlet. Rated at 80% continuous current is 12 amps. 120vac @6.8 ohms is over 17.5 amps.
Jim A

outlet is 120vac 20 amp circuit , I did borrow an amp meter just to check and I was pulling just over 20amps at the plug and just under 20amps at the element

I am still waiting for my new 220v coil from Kiln parts

TZ

 

[Stacy E. Apelt - Bladesmith]

This thread has reminded me of a joke my grandfather (the physicist) told me when I was young:
This man was standing out in front of his house staring at it for an hour. Finally, a neighbor came over and asked what was going on. The man said, "I am trying to decide what paint is best for my house." The neighbor told him he was in luck, because he was a mechanical engineer and knew all about paint. He spent two hours explaining the virtues of latex, vs oil, vs alkyd, vs epoxy, then he went on into the advantage of vinyl siding over aluminum siding as far as maintenance goes. When done he asked the man if he had made a choice. The man said, "Yep, I'm going with white."