Convex grinds

[chiral.grolim]

Pretty much. There is a sliding scale of how important particular details are for practical application purposes. The microscopic end of things would be most relevant to those working, for instance, on developing the next super-steel, sharpening medium, or heat treatment protocol, but not particularly useful to most other folks. The level at which the discussion was originally taking place was one mostly useful to edged tool designers and tinkerers and was already above the level of usefulness to the average knife user.

Shaving, carving wood, planing wood, using a chainsaw ... who would it not be relevant too again?? Useful to everyone, in ANY cutting task. Name one where it isn't relevant? Why are you caught up on the scale? It's the same principle at ANY scale.

 

[FortyTwoBlades]

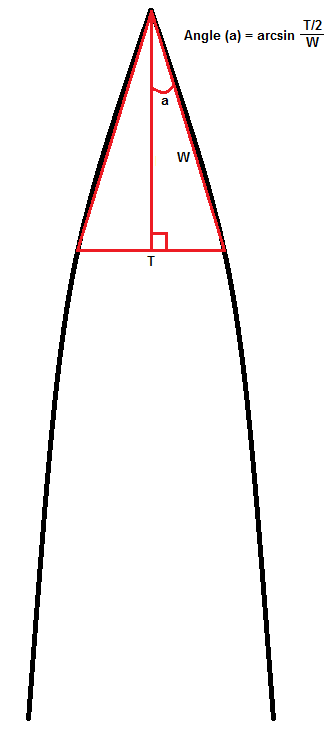
What is the problem you are having? I did not give a scale to the diagram/schematic provided. It could be on the order of microns or of inches, all that matters is that it is representative of the actual bevel AND the apex is sufficiently keen.



Yes it does work, it works at any scale while a tangent does not work at any scale. From your description, the problem lies with where your edge is most convex, i.e. what flat-angle best approximates the cutting performance (to pinnah, it is all about performance, the point of the schematics and micrographs is to dispel confusion about the reality of the performance achieved). What you have described - approaching a flat surface with your edge and not engaging - at what angle are you engaging the surface? You have used a wood-plane, yes? Even with a face-razor on pliable skin, you cannot engage the surface with the bevel flat, it must be elevated. The degree of elevation and the thickness of the bevel (be it flat or convex) determines the depth to which it engages in a cut. Planing wood a common angle of engagement is ~50 degrees with a blade sharpened to >30 degrees inclusive, shaving it's commonly ~30 degrees for a blade sharpened to ~17 degrees inclusive, and most other cutting tasks use an even greater angle to engage. That is practical reality.

Note in the image that the blade has a wear-profile the forms a less acute microbevel as the cut proceeds.

Please note that this diagram was made from a planer on cherry wood (very hard) that continued to engage its target even at the fullest point of wear. Again, since you cannot measure the "tangent" of the convexity, how would you measure the effective edge angle?

Understand that even planing cherry-wood - much stiffer than paper or a pen which you might be using to pretend to test edge-angle - there is enough flexibility in the surface to allow for some penetration (i.e. engagement) despite the progressive loss of clearance, and that convexity is rather dramatic, MUCH more dramatic than what i present in my schematic measuring effective edge angle. To measure the effective edge-angle of the worn planer, you would do as I did before, calculating the angle from the thickness and height of the worn part of the bevel. If you try doing it your way, i.e. checking for engagement at a specific angle, you are really just measuring clearance and flexibility of the material you are cutting and perhaps the keenness of the edge (i.e. diameter of apex), NOT edge angle "effective" or otherwise. Please note, i can shave/engage my facial hairs as well with a 40-degree edge as with a 10-degree edge so long as the edge is sufficiently keen, what is different is the amount of wedging that occurs after the edge has engaged. In an earlier schematic i showed a thick SYKCO 511 and an RMD with the same edge angle, but the SYKCO had less clearance due to the thickness of the bevel behind that of the RMD, so on some material it would have more trouble planing off shavings because the bevel would be up against the material being cut if i laid the blade at a lower angle than the edge, but the RMD might be able to compress the material with the edge-shoulder enough to allow the edge to engage despite being at the same angle, and both were stropped to a convex edge-angle.

I realize all of this. In terms of engaging facial hairs, the medium is still being engaged at an angle in excess of that of the edge angle because deformation of the skin is changing the presentation of the hair relative to the edge...and yes for a held angle the easier it is to deform a surface the easier it is to get an edge to bite at an angle of presentation (to the undeformed surface) less than the actual edge angle, but this testing is best done on targets with relatively low deformation. Deformation itself doesn't alter the fact that the edge cannot and will not bite into a material that isn't presented at an angle in excess of that of the edge...in such a case the the edge is not changing its orientation in space, but the cutting medium is. However, the effective angle will be lowered the softer the material or the greater the force applied.

What you're writing doesn't disagree with my own understanding, but there are practical concerns of debate and there are theoretical ones. Pragmatic solutions come from a marriage of the two in equal measure. The end goal is to cut stuff well, and the effective angle is more meaningful than the one painstakingly measured. Ballpark figures within a relevant range are close enough for the overwhelming majority of individuals. It's all just a matter of how thick a blade is at different points across the distance from edge to spine, and how to optimize the balance between efficiency and resiliency.

 

[FortyTwoBlades]

There's absolutely nothing wrong with theoretical advancement like you're doing, and it's admirable stuff, but my point is more about practical user application. It's good to understand what an edge looks like at that level of magnification from a conceptual standpoint, but when discussing edge angle even a fairly advanced user is probably not going to bust out the microscope every time they want to establish the angle of their edge. That's simply not the scale at which it's practical for them to determine it.

 

[chiral.grolim]

... Deformation itself doesn't alter the fact that the edge cannot and will not bite into a material that isn't presented at an angle in excess of that of the edge...in such a case the the edge is not changing its orientation in space, but the cutting medium is. However, the effective angle will be lowered the softer the material or the greater the force applied.

What you're writing doesn't disagree with my own understanding, but there are practical concerns of debate and there are theoretical ones. Pragmatic solutions come from a marriage of the two in equal measure. The end goal is to cut stuff well, and the effective angle is more meaningful than the one painstakingly measured. Ballpark figures within a relevant range are close enough for the overwhelming majority of individuals. It's all just a matter of how thick a blade is at different points across the distance from edge to spine, and how to optimize the balance between efficiency and resiliency.

I agree with all of this :thumbup:

What i am trying to make clear is:
1) "convex" is by definition thicker than the "flat" angle to which it corresponds at ANY scale, so no more of this "convex is thinner" nonsense, which is literally what it is, "nonsense" as the statement contradicts itself in the language it is being typed.

2) The "effective edge angle" is the one most closely approximated in the manner I have detailed, i.e. measuring thickness and height and calculating. (EDIT: i add that for most cutting implements I simply aim for an angle that is 2X taller than it is thick = 30-degrees inclusive, an easy thing to estimate when sharpening by raising the spine of the blade ~1/4 of the blade width(height) off the hone - steeper is less acute, shallower is more acute. How many people set the angle at 90 or 45 degrees and then estimate from there?)

The method you described which gives a different result depending on the thickness of the bevel and the flexibility of the material being cut is NOT reliable for just those reasons, asserting a theoretical "tangent" to the convexity is also not reliable as it simply ignores reality and has the same issues of measurement that your method has. The challenge with my method which ToddS also uses (though i certainly am not doing this at the microscopic scale) is determining the point at which to measure, but it really isn't all that difficult on the macroscopic scale as obvious transition points are often apparent (e.g. you can see where the bevel shoulders have been rounded down).

Another method is similar to what you have described - paint the bevel with bright red Sharpie and, holding the blade at a known angle (based on height and thickness as previously described), grind off material using a glass/stone hone and then see how close to the apex the paint was removed. You can never actually remove the paint all the way to the very apex without rounding over the apex since, as previously illustrated, the apex is always rounded over, but you simply need to remove paint close enough to the apex that, whatever the angle of the apex its thickness is low enough to give the necessary depth of penetration. That is what is exemplified in the work on planers and also face-razors - the actual apex angle is never as acute as the sharpened bevel-angle, but it is still thin enough to cut into the material anyway at the optimal cutting angle for the task. With a chopping axe, the actual apex can even be quite obtuse so long as the bevel behind it is thin enough to make sufficient penetration to wedge the chopped-material apart.

Using a convex edge puts (actually leaves) more metal behind the edge than a corresponding flat-grind, sacrificing a small amount of ease of penetration near the apex (microbevel) in return for an increase in stiffness/durability.

 

[FortyTwoBlades]

The bevel painting method works fine when you're sharpening, but not so much when it comes to the task of cutting, which is where the effective angle comes into play. There is some degree of variability depending on the specific medium being tested, yes, but the idea is usually to use the hardest target you have at hand (that an edge will actually bit into, of course) and to use minimal pressure, both of which act to keep deformation to a realistic minimum. Because the effective angle is the angle above which the edge will bite on a given material at a given level of force, when it comes to cutting you want to approach the cut above that angle. When sharpening you'll want to back down off the minimum cutting angle just a hair. This method works regardless of if you have a colored permanent marker at your disposal or not.

I still respectfully disagree regarding the geometry thing, but it's a matter of perspective ultimately. Thicker is thicker, thinner is thinner. Thinner cuts better, thicker is stronger.

 

[Rhinoknives1]

I do have one final question?
How many mathematicians does it take to sharpen a knife?

 

[Shotgun]

I do have one final question?
How many mathematicians does it take to sharpen a knife?

How many knife makers does it take to keep a dying thread alive?

 

[REK Knives]

So what do you guys think about a half v half convex edge w/ a hollow primary grind... what would the angle be then?

 

[BenchCo Spydermade]

I agree with all of this :thumbup:

What i am trying to make clear is:
1) "convex" is by definition thicker than the "flat" angle to which it corresponds at ANY scale, so no more of this "convex is thinner" nonsense, which is literally what it is, "nonsense" as the statement contradicts itself in the language it is being typed.

2) The "effective edge angle" is the one most closely approximated in the manner I have detailed, i.e. measuring thickness and height and calculating. (EDIT: i add that for most cutting implements I simply aim for an angle that is 2X taller than it is thick = 30-degrees inclusive, an easy thing to estimate when sharpening by raising the spine of the blade ~1/4 of the blade width(height) off the hone - steeper is less acute, shallower is more acute. How many people set the angle at 90 or 45 degrees and then estimate from there?)

The method you described which gives a different result depending on the thickness of the bevel and the flexibility of the material being cut is NOT reliable for just those reasons, asserting a theoretical "tangent" to the convexity is also not reliable as it simply ignores reality and has the same issues of measurement that your method has. The challenge with my method which ToddS also uses (though i certainly am not doing this at the microscopic scale) is determining the point at which to measure, but it really isn't all that difficult on the macroscopic scale as obvious transition points are often apparent (e.g. you can see where the bevel shoulders have been rounded down).

Another method is similar to what you have described - paint the bevel with bright red Sharpie and, holding the blade at a known angle (based on height and thickness as previously described), grind off material using a glass/stone hone and then see how close to the apex the paint was removed. You can never actually remove the paint all the way to the very apex without rounding over the apex since, as previously illustrated, the apex is always rounded over, but you simply need to remove paint close enough to the apex that, whatever the angle of the apex its thickness is low enough to give the necessary depth of penetration. That is what is exemplified in the work on planers and also face-razors - the actual apex angle is never as acute as the sharpened bevel-angle, but it is still thin enough to cut into the material anyway at the optimal cutting angle for the task. With a chopping axe, the actual apex can even be quite obtuse so long as the bevel behind it is thin enough to make sufficient penetration to wedge the chopped-material apart.

Using a convex edge puts (actually leaves) more metal behind the edge than a corresponding flat-grind, sacrificing a small amount of ease of penetration near the apex (microbevel) in return for an increase in stiffness/durability.

That depends in how you look at the angles.

If you look at the angles corresponding to the apex angle then convex has less metal behind it because it has the same apex angle, but thins more at the shoulders.

If you look at the angle from the edge to the end of the bevel then straight has less metal behind it.

 

[chiral.grolim]

If you look at the angles corresponding to the apex angle then convex has less metal behind it because it has the same apex angle, but thins more at the shoulders.

If you look at the angle from the edge to the end of the bevel then straight has less metal behind it.

Already explained this earlier.
The word "convex" literally means "out from" a corresponding flat that must be thinner - that is English. "Convex" can not ever be thinner than a "corresponding" flat unless you are using the term "corresponding" incorrectly as you just did.
The only way to measure a bevel angle is via measuring the height and thickness and calculating per my previous posts here: http://www.bladeforums.com/forums/showthread.php/1268014-Convex-grinds?p=14540485#post14540485

But again, all should be able to agree that thinner cuts better, thicker is stronger, and THAT is the point of using convex, to achieve a thicker apex for strength.

 

[BenchCo Spydermade]

Already explained this earlier.
The word "convex" literally means "out from" a corresponding flat that must be thinner - that is English. "Convex" can not ever be thinner than a "corresponding" flat unless you are using the term "corresponding" incorrectly as you just did.
The only way to measure a bevel angle is via measuring the height and thickness and calculating per my previous posts here: http://www.bladeforums.com/forums/showthread.php/1268014-Convex-grinds?p=14540485#post14540485

But again, all should be able to agree that thinner cuts better, thicker is stronger, and THAT is the point of using convex, to achieve a thicker apex for strength.

The convex I refer to is more than a word, it is a grind. When I put one on a knife, I TAKE AWAY metal from the flat grind. So worry less about words technical meaning and more about the meaning applied to the convex grind in a knife.

 

[chiral.grolim]

The convex I refer to is more than a word, it is a grind. When I put one in a knife, I TAKE AWAY metal from the flat grind. So worry less about words technical meaning and more on the meaning applied to the convex grind in a knife.

When you take away that metal, do you use a slack-belt grinder like BRKT? If so, you are taking away LESS metal than you would if grinding FLAT on a stone, etc. You ALWAYS TAKE AWAY metal, but it makes a difference how you do it. Again, words.

 

[BenchCo Spydermade]

When you take away that metal, do you use a slack-belt grinder like BRKT? If so, you are taking away LESS metal than you would if grinding FLAT on a stone, etc. You ALWAYS TAKE AWAY metal, but it makes a difference how you do it. Again, words.

What you use to profile an edge makes no difference. The end result is either straight or convex.

Its a chicken or egg thing. But i guess YOU know which came first.

 

[chiral.grolim]

What you use to profile an edge makes no difference. The end result is either straight or convex.

Its a chicken or egg thing. But i guess YOU know which came first.

Added a picture to previous post. You are right, it makes no difference, the corresponding flat is always thinner and requires the removal of more metal.

 

[BenchCo Spydermade]

Added a picture to previous post. You are right, it makes no difference, the corresponding flat is always thinner and requires the removal of more metal.

I don't even touch the edge angle much if at all. , my goal is to preserve the edge angle while thinning/smoothing the transition from bevel to blade.

 

[Rasco]

All this over a Bark River karambit...

 

[Shotgun]

Already explained this earlier.
The word "convex" literally means "out from" a corresponding flat that must be thinner - that is English. "Convex" can not ever be thinner than a "corresponding" flat unless you are using the term "corresponding" incorrectly as you just did.
The only way to measure a bevel angle is via measuring the height and thickness and calculating per my previous posts here: http://www.bladeforums.com/forums/showthread.php/1268014-Convex-grinds?p=14540485#post14540485

But again, all should be able to agree that thinner cuts better, thicker is stronger, and THAT is the point of using convex, to achieve a thicker apex for strength.

You cannot use the arcsin to describe an arc. You're using fuzzy math. Arcsin is a special case for right hand triangles. Which is why you halved the thickness. You are at best APPROXIMATING the angle between the edge and an arbitrary point on avery flat convex. Who decides the width on your diagram for a full convex 0 grind with a heavy arc to it?

 

[chiral.grolim]

You cannot use the arcsin to describe an arc.

I didn't, i used it to describe an angle.

You're using fuzzy math.

No, I'm using the principles of Archimedes, i.e. geometry. I halved the thickness to give the angle in degrees-per-side, that's how it works.

You are at best APPROXIMATING the angle between the edge and an arbitrary point ...

I have stated so repeatedly, and the method of approximation is more reliable, actually measurable, and LESS arbitrary than the approximation made in ways others have suggested. "Tangent" is a non-starter as already explained and even illustrated with micrographs, it's non-viable, and would still only give an approximation albeit a worse one.

Who decides the width on your diagram for a full convex 0 grind with a heavy arc to it?

Really?? What is this problem people are having with scale?? Do you see any scale measurements on that schematic? What about this one (same image stretched):

As I previously noted:

ANGLE is simply an easy way of expressing the distance or thickness between two lines (bevels) at some distance (height/width) back from the vertex (apex).

We have already established through actual micrographs (i.e. reality) that using a theoretical "tangent to the apex" is utterly invalid as the apex-angle is always 90-dps. I do hope people stop bringing it up.

Instead, to establish an "effective edge angle" one must measure the thickness of the blade at some height (or rather bevel-width) back from the apex, usually a distance selected by the presence of an obvious transition point such as a dramatic change in angle (e.g. bevel shoulder) OR as ToddS has done select a height pertinent to the desired cutting performance (he chose 3 microns as that is the approximate thickness of a human hair which razor-blades are designed to cut through with ease).

Once you have these lengths established (width, thickness) you apply geometric principles to give you the "effective edge angle" by drawing a flat sided triangle and then calculating the angle.
...
As may be noted, the "effective edge angle" is simply "the angle measurement of a flat-grind edge that most closely approximates the cutting efficiency of a non-flat edge", and that corresponding flat-grind will ALWAYS fall beneath the convex grind, i.e. flat is always thinner. The level of precision used to establish the effective edge angle, e.g. ToddS's micrographs at 3 micron blade-heights, can be altered depending on the task for which the edge is intended.

You are familiar with Archimedes?

He approximated the value of Pi via inscribing polygons with flat sides to an arc.

Again, "convex" means "out from" a corresponding flat, i.e. it can only correspond to a flat line beneath, thinner.

I don't even touch the edge angle much if at all...

So you are not in fact creating a "convex edge"! You are simply creating a new bevel with a new height and thickness below the old bevel, which would be thinner if you simply used a flat-grind of the same height:

 

[BenchCo Spydermade]

I didn't, i used it to describe an angle.



No, I'm using the principles of Archimedes, i.e. geometry. I halved the thickness to give the angle in degrees-per-side, that's how it works.



I have stated so repeatedly, and the method of approximation is more reliable, actually measurable, and LESS arbitrary than the approximation made in ways others have suggested. "Tangent" is a non-starter as already explained and even illustrated with micrographs, it's non-viable, and would still only give an approximation albeit a worse one.



Really?? What is this problem people are having with scale?? Do you see any scale measurements on that schematic? What about this one (same image stretched):

As I previously noted:


You are familiar with Archimedes?

He approximated the value of Pi via inscribing polygons with flat sides to an arc.

Again, "convex" means "out from" a corresponding flat, i.e. it can only correspond to a flat line beneath, thinner.



So you are not in fact creating a "convex edge"! You are simply creating a new bevel with a new height and thickness below the old bevel, which would be thinner if you simply used a flat-grind of the same height:

OK, I think I can agree with your response to my last post, but how sharp were Archimedes knives?

 

[chiral.grolim]

A principle that should be understood in this discussion is that the apex angle does not really matter, what matters is the apex thickness.

As the micrographs show, the apex of any blade is rounded with a tangent angle 90-dps - perfectly blunt... and yet the knife cuts! Why? because the apex thickness (diameter at this level of precision) is sufficiently small to focus pressure for initiation of the cut. Different materials require different maximum apex thickness to cut. An edge with an apex of 50 microns can carve and chop wood but might not cut cardboard, 20 microns might be effective cutting cardboard but not paper, at 10 microns it might cut paper but not very fine paper or shave hair, at 2 microns it might shave but not very comfortably, etc.,etc. Thinner cuts better.

The thickness of the material behind that apex supports it, and thicker is stronger but reduces cutting efficiency as the material wedges behind the apex. Most knives are beveled at ~5-dps or 10-inclusive which is highly efficient but very weak at thin geometries. This weakness is ameliorated by the addition of secondary bevels close to the apex, common ones include a 15-dps bevel at 0.025 thickness and a 20-dps microbevel at ~0.001 thickness (single swipe on a hone). "Convex" adds variation by smoothing the transition and effectively creating intermediary bevels.
Now, which bevel angle has the greatest import on the cutting geometry of the blade? Here is another schematic of 4 blades, 3 with the same "edge" angle and primary bevel angles that vary no more than 1-dps... but the performance of the three varies greatly. Why?